CUDA N-Body Simulation

In this post, I will analyze the CUDA implementation of the N-Body simulation. The implementation that I will be using as a reference for this article is provided with the CUDA GPU Computing SDK 10.2. The source code for this implementation is available in the “%NVCUDASAMPLES_ROOT%\5_Simulations\nbody” in the GPU Computing SDK 10.2 samples base folder.

I assume the reader has a good understanding of the CUDA programming API.

Contents

1 Introduction
2 Newton’s Law of Universal Gravitation
3 CUDA Implementation
4 Conclusion
5 References

Introduction

The N-Body simulation is a computational simulation that attempts to approximate the evolution of bodies in a system where each body influences all other bodies in the system. Changing any properties of one body have a direct or indirect effect on all other bodies. In this particular example, we consider each body to represent a galaxy or an individual star and each body in the simulation applies a gravitational force all other bodies in the simulation. The distance between two bodies has an influence on the magnitude of that force where bodies that are closer together will apply more force than bodies that are farther apart.

There are several possible approaches we can take to solving this problem. We can use a brute-force, all-pairs N-body simulation where every body computes the gravitational force between all other bodies in the simulation. This implementation has an \(O(n^2)\) complexity, that is, the time it takes to solve the simulation for one unit of time (a time-step) grows exponentially when the number of bodies that need to be simulated grows. For a serial implementation this type of implementation may be prohibitively slow. However, this might be quite reasonable depending on the number of bodies that we can process in parallel.

In this article I will introduce a technique that can be used to solve this problem using a brute-force, all-pairs computation implemented in the NVIDIA CUDA programming API.

Newton’s Law of Universal Gravitation

We will use Newton’s law of universal gravitation to compute the force that is applied between any two bodies. Newton’s law of universal gravitation states that every point mass in the universe attracts every other point mass with a force that is directly proportional to the product of their masses and inversely proportional to the square of the distance between them. This formal definition can be stated analytically as:

\[F=G\frac{m_1m_2}{r^2}\]

Where:

\(F\) is the force acting on each point mass measured in newtons.
\(G\) is the gravitational constant.
\(m_1\) is the mass of the first body measured in kilograms.
\(m_2\) is the mass of the second body measured in kilograms.
\(r\) is the distance between the two bodies in meters (m).

The gravitational constant \(G\) is approximately equal to \(6.674 \times 10^{-11} N m^2kg^{-2}\).

This formula will result in a scalar force measured in newtons, but we are more interested in a 3-dimensional vector that can be applied to move the bodies in 3-dimensional space. For that, we need to determine the direction of the force that should be applied to the two bodies. This is simple if we know the initial positions of the bodies in 3-dimensional space.

Let’s say that one body (\(body_i\)) has a position (\(\mathbf{p}_i\)) in 3D space. A second body (\(body_j\)) has a position (\(\mathbf{p}_j\)), then the vector from \(\mathbf{p}_i\) to \(\mathbf{p}_j\) is:

\[\mathbf{r}_{ij}=\mathbf{p}_j-\mathbf{p}_i\]

We can use this vector to compute a force vector that represent the force that attracts \(body_i\) to \(body_j\).

\[\mathbf{f}_{ij}=G\frac{m_im_j}{\|\mathbf{r}_{ij}\|^2}\cdot\frac{\mathbf{r}_{ij}}{\|\mathbf{r}_{ij}\|}\]

The first part of this formula is recognized as Newton’s law of gravity, the second component is simply the normalized direction vector from \(p_i\) to \(p_j\). The result is a 3-dimensional force vector that can be used to move the bodies together.

The final force (\(\mathbf{F}_i\)) to be applied to \(body_i\) is the sum of all \(N-1\) forces:

\[\mathbf{F}_{i}=\sum_{\substack{1\le{j}\le{N} \\ j\ne{i}}}\mathbf{f}_{ij}=Gm_{i}\cdot\sum_{\substack{1\le{j}\le{N} \\ j\ne{i}}}\frac{m_j\mathbf{r}_{ij}}{\|\mathbf{r}_{ij}\|^{3}}\]

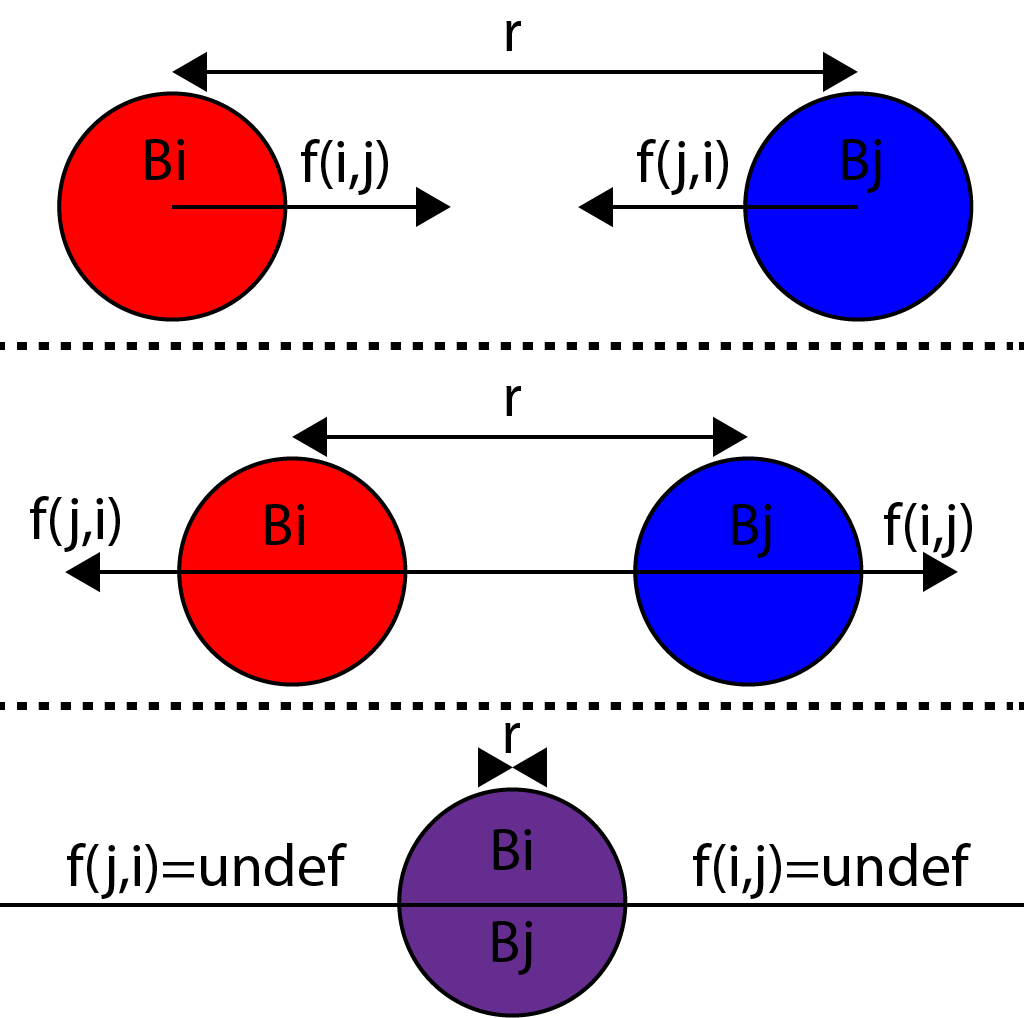
You will notice that this formula only sums forces for unique bodies (where \(i\ne{j}\)). This is a necessity because if two bodies were the same (that is, \(i=j\)) then the distance between them is zero and the denominator becomes zero and as we know from our years of math experience, we can’t divide anything by zero because this results in some undefined result. The acute minded individual might also consider that this situation could occur in our simulation if we don’t prevent two individual bodies from intersecting.

Below shows an example of two bodies that intersect. If the distance between them becomes zero (0), then the forces between them become infinite (undefined).

Body, Body Interaction

The image shows two bodies moving together. As they get closer, the forces pulling them together grows exponentially until the forces become infinite when the two bodies occupy the same space (black hole effect?). However, we don’t want to try to simulate a black hole with this application so ideally, we’d like to prevent the forces from becoming infinite. In order to avoid this scenario, we must introduce a softening factor (\(\epsilon^2 > 0\)) into the denominator and the equation is rewritten as such:

\[\mathbf{F}_i\approx{Gm_i}\cdot\sum_{1\le{j}\le{N}}\frac{m_j\mathbf{r}_{ij}}{\left(\|\mathbf{r}_{ij}\|^2+\epsilon^2\right)^\frac{3}{2}}\]

The softening factor in the denominator limits the magnitude of the forces between the bodies which is desirable when performing numerical integration of the point masses.

To perform the integration step (updating the positions of the bodies in space for a single time-step), we need the acceleration to apply to each body. We can rewrite the equation to solve for acceleration directly using the following formula:

\[\mathbf{a}_i\approx{G}\cdot\sum_{1\le{j}\le{N}}\frac{m_j\mathbf{r}_{ij}}{\left(\|\mathbf{r}_{ij}\|^2+\epsilon^2\right)^\frac{3}{2}}\]

Notice that we have now removed the \(j\ne{i}\) condition from the sum above. This is because \(\mathbf{f}_{ij}=0\) where \(i=j\) if \(\epsilon^2 > 0\). In this case, \(\mathbf{r}_{ij}=0\) making the numerator zero.

CUDA Implementation

In this article, I will only discuss the details of the CUDA implementation. If you want to see how to setup a project that uses CUDA, you can refer to my previous article titled Introduction to CUDA and if you want to see how to execute a CUDA kernel, then you can refer to my previous article title CUDA Execution Model.

If you remember from the article on the CUDA Execution Model a CUDA grid consists of one ore more thread blocks that are further divided into one or more threads. Threads within a thread-block can be arranged into 1-, 2-, or 3-dimensions and a grid of thread-blocks can be arranged into 1-, or 2-dimensions (3-dimensions on devices that support compute capability 2.0). For this implementation we will use a grid of 1-Dimensional thread blocks where each thread will process a single body in the simulation.

Since we also want to minimize the accesses to global memory, then we will also utilize shared memory to speed-up the implementation. Using shared memory to speed-up a CUDA application was described in a previous article title CUDA Memory Model. Since we can’t fit the entire input data into shared memory at the same time (because of the limited amount of shared memory that each streaming multiprocessor has) we need to “tile” the input data. The basic idea is, we will split the input data into groups of data called tiles. The first tile of input data is loaded into shared memory and that data is processed, then we load the next tile of data into shared memory then processes it. We repeat this process until the entire set of input data is processed. This tiling process can be synchronized within a thread block. Every thread in the thread block has access to the shared memory and uses it to compute the forces applied to each body in the simulation.

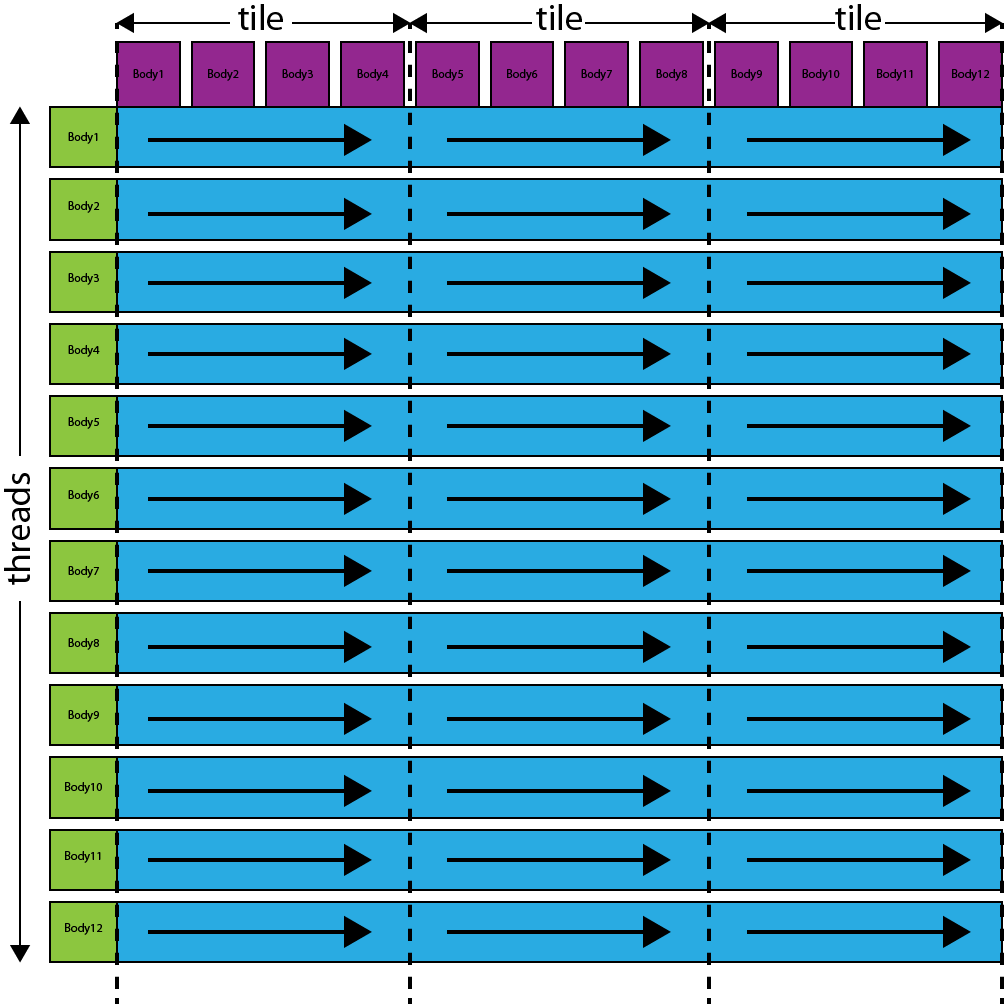
The image below shows how we might visualize this process.

N-Body Threads

This image shows the threads in a thread block on the vertical axis. Each thread computes the total acceleration that is applied to the body represented by that thread. The dashed vertical lines represent synchronization points where a tile of global memory is loaded into the shared memory buffer. At the first synchronization point, the definitions of the first four bodies are loaded into shared memory. Then, each thread in the block will process the first four bodies from the shared memory buffer, computing the acceleration applied to the body represented by the thread. At the next synchronization point, the next four bodies are loaded and processed. This process continues until all bodies have been processed.

Of course, this image only shows a theoretical representation of the actual input data. In reality, there will be thousands of bodies being processed and therefor thousands of threads each processing thousands of bodies.

Calculate Forces Kernel Function

Let’s see how we might implement this in the CUDA kernel. Below we see the entry point for the kernel function that is invoked on the host:

__global__ void calculate_forces(float4* globalX, float4* globalA)
{
  // A shared memory buffer to store the body positions.
  extern __shared__ float4[] shPosition;
  
  float4 myPosition;
  int i, tile;

  float3 acc = {0.0f, 0.0f, 0.0f};
  // Global thread ID (represent the unique body index in the simulation) 
  int gtid = blockIdx.x * blockDim.x + threadIdx.x;

  // This is the position of the body we are computing the acceleration for.
  float4 myPosition = globalX[gtid];

  for (i = 0, tile = 0; i < N; i += blockDim.x, tile++) 
  {
    int idx = tile * blockDim.x + threadIdx.x;

    // Each thread in the block participates in populating the shared memory buffer.
    shPosition[threadIdx.x] = globalX[idx];
    // Synchronize guarantees all thread in the block have updated the shared memory
    // buffer.
    __syncthreads();

    acc = tile_calculation(myPosition, acc);

    // Synchronize again to make sure all threads have used the shared memory
    // buffer before we overwrite the values for the next tile.
    __syncthreads();
  }
  
  // Save the total acceleration in global memory for the integration step.
  float4 acc4 = {acc.x, acc.y, acc.z, 0.0f};
  globalA[gtid] = acc4;
}

__global__ void calculate_forces(float4* globalX, float4* globalA)

{

// A shared memory buffer to store the body positions.

extern __shared__ float4[] shPosition;

float4 myPosition;

int i, tile;

float3 acc = {0.0f, 0.0f, 0.0f};

// Global thread ID (represent the unique body index in the simulation)

int gtid = blockIdx.x * blockDim.x + threadIdx.x;

// This is the position of the body we are computing the acceleration for.

float4 myPosition = globalX[gtid];

for (i = 0, tile = 0; i < N; i += blockDim.x, tile++)

{

int idx = tile * blockDim.x + threadIdx.x;

// Each thread in the block participates in populating the shared memory buffer.

shPosition[threadIdx.x] = globalX[idx];

// Synchronize guarantees all thread in the block have updated the shared memory

// buffer.

__syncthreads();

acc = tile_calculation(myPosition, acc);

// Synchronize again to make sure all threads have used the shared memory

// buffer before we overwrite the values for the next tile.

__syncthreads();

}

// Save the total acceleration in global memory for the integration step.

float4 acc4 = {acc.x, acc.y, acc.z, 0.0f};

globalA[gtid] = acc4;

}

The calculate_forces CUDA kernel function takes two arguments, the first parameter globalX stores the positions of all N-bodies in the simulation in global memory. The second parameter globalA stores the current accelerations of the bodies in global memory.

The shPosition shared memory buffer declared on line 4 is used to reduce access to global memory.

On line 11, the global thread ID (gtid) is computed based on the current block ID and thread ID. The global thread ID is used to determine which body this thread is processing.

On line 14, the position of the current body is “cached” in a register variable (myPosition) for faster access.

The for-loop on line 16 is used to perform the tile calculation (shown in blue in the “N-Body threads” image above).

The first step is to populate the shared memory buffer. This is done by allowing each thread in the block to write one value from global memory into the shared memory buffer. On line 24, the threads in the block are synchronized at which point the entire tile should be available in shared memory.

The tile_calculation device function will compute the acceleration that is applied to the current body (myPosition). The function will accumulate the accelerations of all the other bodies in the current tile.

On line 30, the thread block is synchronized again which guarantees that all threads are finished using the shared memory buffer before it is overwritten by the next tile.

After all of the tiles have been processed, the final accumulated acceleration is then written to the globalA acceleration global memory buffer. This value will be used to update the positions of the bodies in another kernel function.

We could integrate the accelerations into the bodies directly if we had another buffer to store the new positions (one buffer for the current positions, and another for the updated positions). We can’t integrate the body positions into the same buffer we are reading from because some threads will be computed after this one and we need to guarantee the bodies will not be modified until all threads have processed all bodies. So using a single buffer for the positions requires that we integrate the accelerations in a separate kernel function only after this kernel function has processed all bodies.

Tile Calculation Device Function

Let’s take look at what the tile_calculation function would look like.

 __device__ float3 tile_calculation(float4 myPosition, float3 accel)
{
  int i;
  extern __shared__ float4[] shPosition;

  for (i = 0; i < blockDim.x; i++) 
  {
    accel = bodyBodyInteraction(myPosition, shPosition[i], accel);
  }
  
  return accel;
}

__device__ float3 tile_calculation(float4 myPosition, float3 accel)

{

int i;

extern __shared__ float4[] shPosition;

for (i = 0; i < blockDim.x; i++)

{

accel = bodyBodyInteraction(myPosition, shPosition[i], accel);

}

return accel;

}

This simple function takes the position of the current body (myPosition) and the current acceleration accel as it’s parameters.

The shared memory buffer declared on line 43 refers to the same shared memory buffer that was declared in the calculate_forces kernel function. We assume that it was already populated so we can just use it in this function.

The for-loop on line 45 loops through all of the body positions in the tile, accumulating the accelerations that will be applied on the body represented by the myPosition argument.

On line 50, the accumulated acceleration is returned to the calling function.

Computing the Acceleration

The bodyBodyInteraction device function will compute the acceleration (\(a_i\)) of one body (\(body_i\)) based on another body (\(body_j\)) using the formula discussed earlier.

__device__ float3 bodyBodyInteraction(float4 bi, float4 bj, float3 ai)
{
  float3 r;

  // r_ij  [3 FLOPS]
  r.x = bj.x - bi.x;
  r.y = bj.y - bi.y;
  r.z = bj.z - bi.z;

  // distSqr = dot(r_ij, r_ij) + EPS^2  [6 FLOPS]
  float distSqr = r.x * r.x + r.y * r.y + r.z * r.z + EPS2;

  // invDistCube =1/distSqr^(3/2)  [4 FLOPS (2 mul, 1 sqrt, 1 inv)]
  float distSixth = distSqr * distSqr * distSqr;
  float invDistCube = 1.0f/sqrtf(distSixth);

  // s = m_j * invDistCube [1 FLOP]
  float s = bj.w * invDistCube;

  // a_i =  a_i + s * r_ij [6 FLOPS]
  ai.x += r.x * s;
  ai.y += r.y * s;
  ai.z += r.z * s;

  return ai;
}

__device__ float3 bodyBodyInteraction(float4 bi, float4 bj, float3 ai)

{

float3 r;

// r_ij [3 FLOPS]

r.x = bj.x - bi.x;

r.y = bj.y - bi.y;

r.z = bj.z - bi.z;

// distSqr = dot(r_ij, r_ij) + EPS^2 [6 FLOPS]

float distSqr = r.x * r.x + r.y * r.y + r.z * r.z + EPS2;

// invDistCube =1/distSqr^(3/2) [4 FLOPS (2 mul, 1 sqrt, 1 inv)]

float distSixth = distSqr * distSqr * distSqr;

float invDistCube = 1.0f/sqrtf(distSixth);

// s = m_j * invDistCube [1 FLOP]

float s = bj.w * invDistCube;

// a_i = a_i + s * r_ij [6 FLOPS]

ai.x += r.x * s;

ai.y += r.y * s;

ai.z += r.z * s;

return ai;

}

On line 57-60, the distance between the two bodies (\(\mathbf{r}_{ij}\)) is computed.

The denominator of the formula is computed on lines 63-67. The value EPS2 is the constant softening factor that is used to prevent divide-by-zero errors in the case where \(\mathbf{r}_{ij}=0\).

The bj.w component is used to store the mass of \(body_j\). It is used as the numerator for the gravitational formula.

On line 73-75, the distance between \(body_i\) and \(body_j\) is integrated into the current acceleration of \(body_i\) and on line 77, the accumulated acceleration is returned to the calling function.

Conclusion

This implementation of the N-Body simulation shown here is a very simple solution to this problem. There are several additional optimizations that can be made that aren’t shown here. For example, for simulations that consist of less than 1024 bodies, thread blocks consisting of 256 threads will only result in 1024/256 = 4 thread blocks. For a system with 8 streaming multiprocessors, this will only result in half of the streaming multiprocessors being used and each streaming multiprocessor will only have 256 of a total 1024 active threads running on each one. This is not optimal but we could improve this if we allow a single body to be updated by multiple threads in the same block. This would result in each thread only updating a fraction of the bodies in the system, but all threads together will process all bodies. This would also result in more scheduled thread blocks per streaming multiprocessors and therefor higher occupancy. For simulations with more than 2048 bodies, there may be little to no gain from allowing multiple threads to process a single body.

References

For a full analysis of this algorithm, I would refer you to Chapter 31. “Fast N-Body Simulation with CUDA” in the GPU Gems 3 book.

The NVIDIA GPU Computing SDK can be obtained from the CUDA Toolkit download page. The GPU Computing SDK contains source code for the N-Body simulation using both CUDA and OpenCL.

3 thoughts on “CUDA Case Study – N-Body Simulation”

JuanJo on February 5, 2012 at 1:00 pm said:

Very useful information and very well explained. I had read the chapter “Fast N-Body Simulation with CUDA” but I did not understand all concepts. This work is useful for my final project of Computer Science. I will write your blog in my references.

Thank you.

Reply ↓
Filipo on July 20, 2012 at 11:48 pm said:

Nice paper! You made easy to understand the thinking behind the nvidia paper. But I would like to ask you few questions:

– what about shared memory allocation? How much memory we have to allocate on shared memory?
– “tiles” have the same size (I mean, the same amount of bodies) wich a blockDim.y can contain? I thought that nvidia had used an “q” dimension to size those tiles.

Maybe if you would include a example on how to call the kernel (and allocating shared memory previously of this) would be perfect!

Congratulations! Cheers!

Reply ↓
- Jeremiah van Oosten on September 21, 2012 at 9:37 am said:
  Filipo,
  
  Please refer to my previous articles about CUDA:
  - CUDA Thread Execution Model
  - CUDA Memory Model
  And the other CUDA related articles can be found here: CUDA
  Reply ↓

3D Game Engine Programming

Helping you build your dream game engine

CUDA Case Study – N-Body Simulation