In this tutorial, you will be introduced to game physics. This is an incredibly broad field, and quite complex too, so you’ll really only get a teaser. This will however produce some pretty neat effects.
Previous Part: File I/ONext Part: AI
Getting Started
For this tutorial, we’ll be using the same template from the 2nd tutorial:
Physics
Many recent games use highly advanced physics engines. A physics engine is a piece of software that gets linked to a game. It takes care of natural behaviour of objects in the game, taking into account forces, collisions, momentum, rotation and torque. Writing a good physics engine is hard for a number of reasons:
- Some game objects move fast, which makes accurate calculations tricky;
- Simulation in a game happens in steps, rather than continuously, like in nature.
For this tutorial, we will therefore focus on a simplified physics model, called Verlet Integration.
Verlet Integration
It works like this. If you have an object that moves along a straight line at a fixed speed, for each frame of your game, you can calculate its position like this:
\[p=o+v\Delta{t}\]
Where:
- \(p\) is the new position of the object
- \(o\) is the origin of the object
- \(v\) is the speed (or velocity) the object is moving
- \(\Delta{t}\) is the change in time since it was at the origin
That’s one way. Another way just looks at subsequent frames, and calculates the position incrementally:
\[p\mathrel{+}=v\Delta{t}\]
If the time it takes to render one frame is roughly the same each time, you can simplify this one step further:
\[
\begin{array}{rcl}
\Delta{p} & = & (p-p_0) \\
p_0 & = & p \\
p & \mathrel{+}= & \Delta{p} \\
\end{array}
\]
Where:
- \(p_0\) is the position of the object in the previous frame
- \(\Delta{p}\) is the change of position from the previous frame
In other words: If we moved an object from \(p_0\) to \(p\) during the previous frame and both \(\Delta{t}\) and \(v\) remain the same, then we will move the same distance for the current frame. The distance between two snapshots now effectively becomes the object’s velocity.
Now imagine that there is a force that is pulling on our object (e.g. gravity). To apply that force, we adjust the position (by adding \(\Delta{p}\)) and then we move the object some more, to account for this force. If the object was already moving down, it will now move down faster, because in the next frame, \(\Delta{p}\) includes the applied gravity.
Let’s put this into some code. Replace game.cpp with:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 |
#include "game.h" #include "surface.h" #include "template.h" #include "windows.h" namespace Tmpl8 { void Game::Init() {} void Game::Shutdown() {} void Game::Tick(float deltaTime) { } }; |
First, I need a piece of code to draw a circle. That’s because circles (and spheres, in 3D) are excellent for physics. You’ll soon enough find out why.
|
8 9 10 11 12 13 14 15 16 |
void Circle( Surface* s, float x, float y, float r ) { for ( int i = 0; i < 64; i++ ) { float r1 = (float)i * PI / 32, r2 = (float)(i + 1) * PI / 32; s->Line( x - r * sinf( r1 ), y - r * cosf( r1 ), x - r * sinf( r2 ), y - r * cosf( r2 ), 0xff0000 ); } } |
No need to scrutinise that code, for now it’s fine to simply use it.
Then, the falling ball code, using Verlet integration:
|
21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 |
float x[2] = { 300, 320 }, y[2] = { 0, ScreenHeight - 50 }; float px[2] = { 300, 320 }, py[2] = { 0, ScreenHeight - 50 }; void Game::Tick(float deltaTime) { screen->Clear(0); Circle(screen, x[0], y[0], 16); Circle(screen, x[1], y[1], 49); // compute deltas. float dx = x[0] - px[0], dy = y[0] - py[0]; // store previous position. px[0] = x[0], py[0] = y[0]; // Verlet integration x[0] += dx; y[0] += dy; // add force due to gravity. y[0] += 0.5f; // delay Sleep(50); } |
As you can see, the ball starts falling, and its velocity is increasing. It does fall through the floor though… And let’s not forget the other sphere.
Verlet Constraints
So, we now have subsequent positions (the difference of which is the velocity), and forces (implemented by changing positions directly on line 37). We need one more thing: constraints. In nature, a ball cannot fall through another ball, or through the floor. Using Verlet integration, we handle this using constraints.
Here’s one example: Since a ball cannot fall through the floor, we need to test for that. As soon as we detect that a ball does intersect the floor, we correct the situation, by moving the ball out of the floor. Note that this effectively changes the speed of the ball, if we keep interpreting the difference between subsequent positions as speed!
Apart from avoiding collisions using constraints, we can also keep objects together, using simple springs. This time, the constraint is: Two objects may not be further apart than a certain distance. When they are, we move both objects closer together to simulate the spring.
So, let’s add a first constraint. Here’s the code:
|
24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 |
void Game::Tick(float deltaTime) { screen->Clear(0); Circle(screen, x[0], y[0], 16); Circle(screen, x[1], y[1], 49); // compute deltas. float dx = x[0] - px[0], dy = y[0] - py[0]; // store previous position. px[0] = x[0], py[0] = y[0]; // Verlet integration x[0] += dx; y[0] += dy; // add force due to gravity. y[0] += 0.5f; // constraints if (y[0] > (ScreenHeight - 17)) y[0] = ScreenHeight - 17; // delay Sleep(50); } |
The result may be a bit unsatisfying. No bouncing? We can improve it a little bit:
|
24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 |
void Game::Tick(float deltaTime) { screen->Clear(0); Circle(screen, x[0], y[0], 16); Circle(screen, x[1], y[1], 49); // compute deltas. float dx = x[0] - px[0], dy = y[0] - py[0]; // store previous position. px[0] = x[0], py[0] = y[0]; // Verlet integration x[0] += dx; y[0] += dy; // add force due to gravity. y[0] += 0.5f; // constraints if (y[0] > (ScreenHeight - 17)) py[0] = y[0], y[0] = ScreenHeight - 17; // delay Sleep(50); } |
But that’s a hack. In general, Verlet integration is not very good for bounces, sadly. Let’s see what it is good at: The other sphere.
Sphere-Sphere Collision
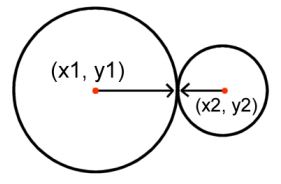
How can we determine if the two balls are colliding? We need some math for that. If ball \(1\) is located at \((x_1,y_1)\), and ball \(2\) is located at \((x_2,y_2)\), then the distance is \(\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}\). If this distance is less than the sum of their radii (radiuses), then they are intersecting.
When the circles intersect, we have a number of options.
- We could move the smallest ball, so that it doesn’t intersect anymore;
- We could move both balls;
- We could move both balls, but the lightest ball more than the heavier one.
Option 3 is clearly the most realistic one. But how do we move the balls away from each other? Maths to the rescue again: If the circles intersect, their distance is smaller than their combined radii. The combined radii minus their distance is the penetration depth, and thus the distance they need to be moved apart. Now, if the small ball is ten times lighter than the large one, the small one will do 90% of this distance, and the big one only 10%. Here we go:
|
24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 |
void Game::Tick(float deltaTime) { screen->Clear(0); Circle(screen, x[0], y[0], 16); Circle(screen, x[1], y[1], 49); // compute deltas. float dx = x[0] - px[0], dy = y[0] - py[0]; // store previous position. px[0] = x[0], py[0] = y[0]; // Verlet integration x[0] += dx; y[0] += dy; // add force due to gravity. y[0] += 0.5f; // constraints if (y[0] > (ScreenHeight - 17)) py[0] = y[0], y[0] = ScreenHeight - 17; float xdist = x[1] - x[0]; float ydist = y[1] - y[0]; float distance = sqrtf(xdist * xdist + ydist * ydist); if (distance < (16 + 49)) { float fix = (16 + 49) - distance; float fraction = fix / distance; x[0] -= fraction * xdist; y[0] -= fraction * ydist; } // delay Sleep(50); } |
In words: for two balls with radii \(16\) and \(49\), the distance should be at least \(16 + 49\). If it isn’t, then they are intersecting, by \((16 + 49) – d\), where \(d\) is the distance between the two balls. They need to be moved apart, and not just in any direction, but along the line that connects their centres.
Once that is done, the small ball responds surprisingly realistic to the collision.
Assignment
There is clearly a very large amount of experiments that you could carry out with this code, so today’s assignment is a somewhat random selection.
- Fix the code so that the big ball moves. Assume that it is heavier than the small ball.
- Add vertical walls, so that the small ball doesn’t leave the screen anymore.
- Add some extra small balls. Make sure that all balls collide with all other balls. Do not forget that a ball should not collide with itself.
- Add a spring: Connect a heavy ball to a fixed point, and if it gets further than a preset distance from that point, pull it towards the point using Verlet physics.
Let it rain… At some point, you will bring C/C++ to its knees. How to make code like this faster is a topic for another day…


 TheTemplate.zip
TheTemplate.zip