In this article I will attempt to explain the concept of Quaternions in an easy to understand way. I will explain how you might visualize a Quaternion as well as explain the different operations that can be applied to quaternions. I will also compare applications of matrices, euler angles, and quaternions and try to explain when you would want to use quaternions instead of Euler angles or matrices and when you would not.
Contents
- 1 Introduction
- 2 Complex Numbers
- 3 Powers of \(i\)
- 4 The Complex Plane
- 5 Quaternions
- 5.1 Quaternions as an Ordered Pair
- 5.2 Adding and Subtracting Quaternions
- 5.3 Quaternion Products
- 5.4 A Real Quaternion
- 5.5 Multiplying a Quaternion by a Scalar
- 5.6 Pure Quaternions
- 5.7 Additive Form of a Quaternion
- 5.8 Unit Quaternion
- 5.9 Binary Form of a Quaternion
- 5.10 Quaternion Conjugate
- 5.11 Quaternion Norm
- 5.12 Quaternion Normalization
- 5.13 Quaternion Inverse
- 5.14 Quaternion Dot Product
- 6 Rotations
- 7 Quaternion Interpolation
- 8 Conclusion
- 9 Download the Demo
- 10 Reference
This article is extremely math intensive and is not intended for the weak-hearted.
Introduction
In computer graphics, we use transformation matrices to express a position in space (translation) as well as its orientation in space (rotation). Optionally, a single transformation matrix can also be used to express the scale or “shear” of an object. We can think of this transformation matrix as a “basis space” where if you multiply a vector or a point (or even another matrix) by a transformation matrix you “transform” that vector, point or matrix into the space represented by that matrix.
In this article, I will not discuss the details of transformation matrices. For a detailed description of transformation matrices, you can refer to my previous article titled Matrices.
In this article, I want to discuss an alternative method of describing the orientation of an object (rotation) in space using quaternions.
The concept of quaterinions was realized by the Irish mathematician Sir William Rowan Hamilton on Monday October 16th 1843 in Dublin, Ireland. Hamilton was on his way to the Royal Irish Academy with his wife and as he was passing over the Royal Canal on the Brougham Bridge he made a dramatic realization that he immediately carved into the stone of the bridge.
\[i^2=j^2=k^2=ijk=-1\]

William Rowan Hamilton Plaque on Broome Bridge on the Royal Canal commemorating his discovery of the fundamental formula for quaternion multiplication.
Complex Numbers
Before we can fully understand quaterions, we must first understand where they came from. The root of quaternions is based on the concept of the complex number system.
In addition to the well-known number sets (Natural, Integer, Real, and Rational), the Complex Number system introduces a new set of numbers called imaginary numbers. Imaginary numbers were invented to solve certain equations that had no solutions such as:
\[x^2+1=0\]
To solve this expression, we must state that \(x^2=-1\) which we know is not possible because the square of any number (positive or negative) is always positive.
Mathematicians generally can’t accept that an expression does not have a solution so a new term was invented called the imaginary number that can be used to solve such equations.
The imaginary number has the form:
\[i^2=-1\]
Don’t try to actually understand this term as there is no logical reason why it exists. We just have to accept that \(i\) is just something that squares to \(-1\).
The set of imaginary numbers can be represented by \(\mathbb{I}\).
The set of complex numbers (represented by the symbol \(\mathbb{C}\)) is the sum of a real number and an imaginary number and has the form:
\[z=a+bi~~a,b\in\mathbb{R},~~i^2=-1\]
It could also be stated that all Real numbers are complex numbers with \(b=0\) and all imaginary numbers are complex numbers with \(a=0\).
Adding and Subtracting Complex Numbers
Complex numbers can be added and subtracted by adding or subtracting the real, and imaginary parts.
Addition:
\[(a_1+b_1i)+(a_2+b_2i)=(a_1+a_2)+(b_1+b_2)i\]
Subtraction:
\[(a_1+b_1i)-(a_2+b_2i)=(a_1-a_2)+(b_1-b_2)i\]
Multiply a Complex Number by a Scalar
A complex number is multiplied by a scalar by multiplying each term of the complex number by the scalar:
\[\lambda(a+bi)=\lambda{a}+\lambda{b}i\]
Product of Complex Numbers
Complex numbers can also be multiplied by applying normal algebraic rules.
\[\begin{array}{rcl}z_1 & = & (a_1+b_1i) \\ z_2 & = & (a_2+b_2i) \\ z_1z_2 & = & (a_1+b_1i)(a_2+b_2i) \\ & = & a_1a_2+a_1b_2i+b_1a_2i+b_1b_2i^2 \\ & = & (a_1a_2-b_1b_2)+(a_1b_2+b_1a_2)i\end{array}\]
Square of Complex Numbers
A complex number can also be squared by multiplying by itself:
\[\begin{array}{rcl}z & = & (a+bi) \\ z^2 & = & (a+bi)(a+bi) \\ & = & (a^2-b^2)+2abi\end{array}\]
Complex Conjugate
The conjugate of a complex number is a complex number with the imaginary part negated and is denoted as either \(\bar{z}\) or \(z^*\).
\[\begin{array}{rcl}z & = & (a+bi) \\ z^* & = & (a-bi)\end{array}\]
The product of a complex number and its conjugate gives a special result.
\[\begin{array}{rcl}z & = & (a+bi) \\ z^* & = & (a-bi) \\ zz^* & = & (a+bi)(a-bi) \\ & = & a^2-abi+abi+b^2 \\ & = & a^2+b^2\end{array}\]
Absolute Value of a Complex Number
We can use the conjugate of a complex number to compute the absolute value (or norm, or magnitude) of a complex number. The absolute value of a complex number is the square-root of the complex number multiplied by its conjugate and is denoted \(|z|\):
\[\begin{array}{rcl}z & = & (a+bi) \\ |z| & = & \sqrt{zz^*} \\ & = & \sqrt{(a+bi)(a-bi)} \\ & = & \sqrt{a^2+b^2}\end{array}\]
Quotient of Two Complex Numbers
To compute the quotient of two complex numbers, we multiply the numerator and denominator by the complex conjugate of the denominator.
\[\begin{array}{rcl}z_1 & = & (a_1+b_1i) \\ z_2 & = & (a_2+b_2i) \\ \cfrac{z_1}{z_2} & = & \cfrac{a_1+b_1i}{a_2+b_2i} \\ & = & \cfrac{(a_1+b_1i)(a_2-b_2i)}{(a_2+b_2i)(a_2-b_2i)} \\ & = & \cfrac{a_1a_2-a_1b_2i+b_1a_2i-b_1b_2i^2}{a_2^2+b_2^2} \\ & = & \cfrac{a_1a_2+b_1b_2}{a_2^2+b_2^2}+\cfrac{b_1a_2-a_1b_2}{a_2^2+b_2^2}i \end{array}\]
Powers of \(i\)
If we state that \(i^2=-1\) then it should be possible to raise \(i\) to other powers as well.
\[\begin{array}{rrrrrrr}i^0 & = & & & & & 1 \\ i^1 & = & & & & & i \\ i^2 & = & & & & & -1 \\ i^3 & = & ii^2 & = & & & -i \\ i^4 & = & i^{2}i^{2} & = & & & 1 \\ i^5 & = & ii^4 & = & & & i \\ i^6 & = & ii^5 & = & i^2 & = & -1\end{array}\]
If we keep writing this sequence, we will see a pattern emerge \((1,i,-1,-i,1,\dots)\).
A similar pattern emerges from the increasing negative powers.
\[\begin{array}{rcr}i^0 & = & 1 \\ i^{-1} & = & -i \\ i^{-2} & = & -1 \\ i^{-3} & = & i \\ i^{-4} & = & 1 \\ i^{-5} & = & -i \\ i^{-6} & = & -1\end{array}\]
You may have seen a similar pattern in mathematics before but in the form \((x,y,-x,-y,x,\dots)\) which is generated by rotating a point 90° counter-clockwise on a 2D Cartesian plane and the sequence \((x,-y,-x,y,x,\dots)\) is generated by rotating a point 90° clockwise on a 2D Cartesian plane.
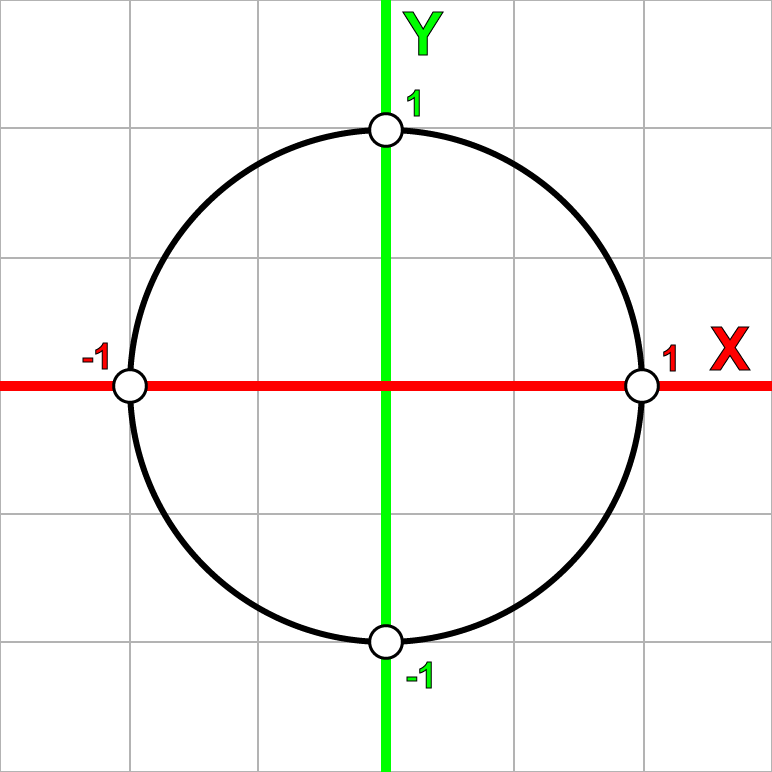
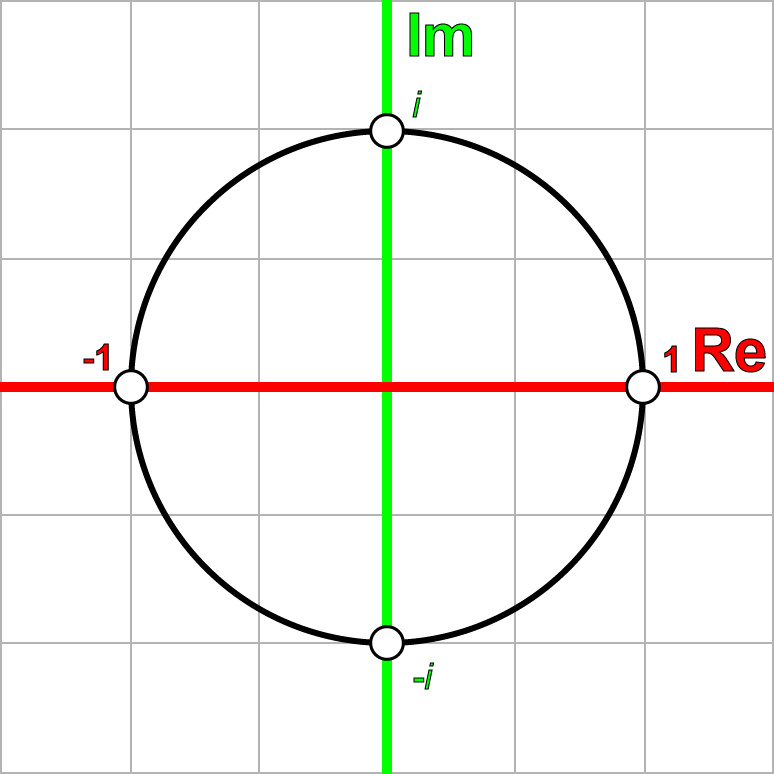
The Complex Plane
We can also map complex numbers in a 2D grid called the Complex Plane by mapping the Real part on the horizontal axis and the Imaginary part on the vertical axis.
As shown in the previous sequence, we can say that if we multiply a complex number by \(i\), we can rotate the complex number through the complex plane at 90° increments.
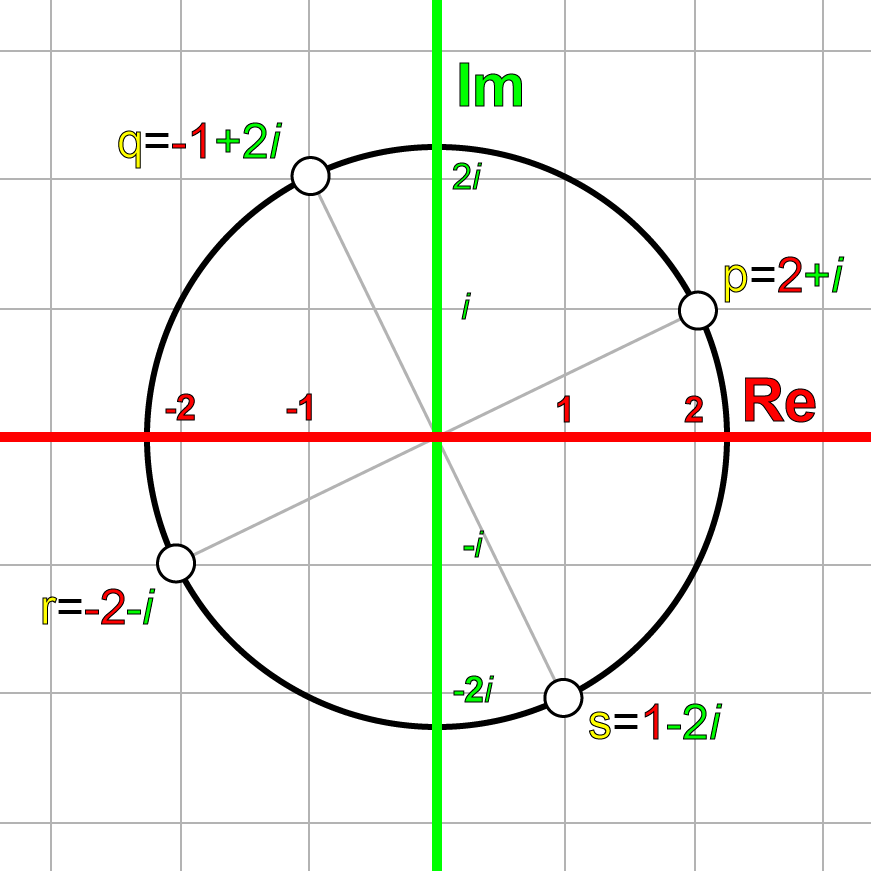
Let’s see if this is true. We’ll take an arbitrary point \(p\) in the complex plane:
\[p=2+i\]
and we multiply it by \(i\) gives \(q\):
\[\begin{array}{rcl}p & = & 2+i \\ q & = & pi \\ & = & (2+i)i \\ & = & 2i+i^2 \\ & = & -1+2i\end{array}\]
Multiplying \(q\) by \(i\) gives \(r\):
\[\begin{array}{rcl}q & = & -1+2i \\ r & = & qi \\ & = & (-1+2i)i \\ & = & -i+2i^2 \\ & = & -2-i\end{array}\]
And multiplying \(r\) by \(i\) gives \(s\):
\[\begin{array}{rcl}r & = & -2-i \\ s & = & ri \\ & = & (-2-i)i \\ & = & -2i-i^2 \\ & = & 1-2i\end{array}\]
And multiplying \(s\) by \(i\) gives \(t\):
\[\begin{array}{rcl}s & = & 1-2i \\ t & = & si \\ & = & (1-2i)i \\ & = & i-2i^2 \\ & = & 2+i\end{array}\]
Which is exactly what we started with (\(p\)). If we plot these complex numbers on the complex plane, we get the following result.
We can also rotate clock-wise in the complex plane by multiplying the complex number by \(-i\).
Rotors
We can also perform arbitrary rotations in the complex plane by defining a complex number of the form:
\[q=\cos\theta+i\sin\theta\]
Multiplying any complex number by the rotor \(q\) produces the general formula:
\[\begin{array}{rcl} p & = & a + bi \\ q & = & \cos\theta+i\sin\theta \\ pq & = & (a+bi)(\cos\theta+i\sin\theta) \\ a^{\prime}+b^{\prime}i & = & a\cos\theta-b\sin\theta+(a\sin\theta+b\cos\theta)i \end{array}\]
Which can also be written in matrix form:
\[\begin{bmatrix} a^{\prime} & -b^{\prime} \\ b^{\prime} & a^{\prime} \end{bmatrix}=\begin{bmatrix} \cos\theta & -\sin\theta \\ \sin\theta & \cos\theta \end{bmatrix}\begin{bmatrix}a & -b \\b & a \end{bmatrix}\]
Which is the method to rotate an arbitrary point in the complex plane counter-clockwise about the origin.
Quaternions
With this knowledge of the complex number system and the complex plane, we can extend this to 3-dimensional space by adding two imaginary numbers to our number system in addition to \(i\).
The general form to express quaternions is
\[q=s+xi+yj+zk~~s,x,y,z\in\mathbb{R}\]
Where, according to Hamilton’s famous expression:
\[i^2=j^2=k^2=ijk=-1\]
and
\[\begin{array}{ccc}ij=k & jk=i & ki=j \\ ji=-k & kj=-i & ik=-j\end{array}\]
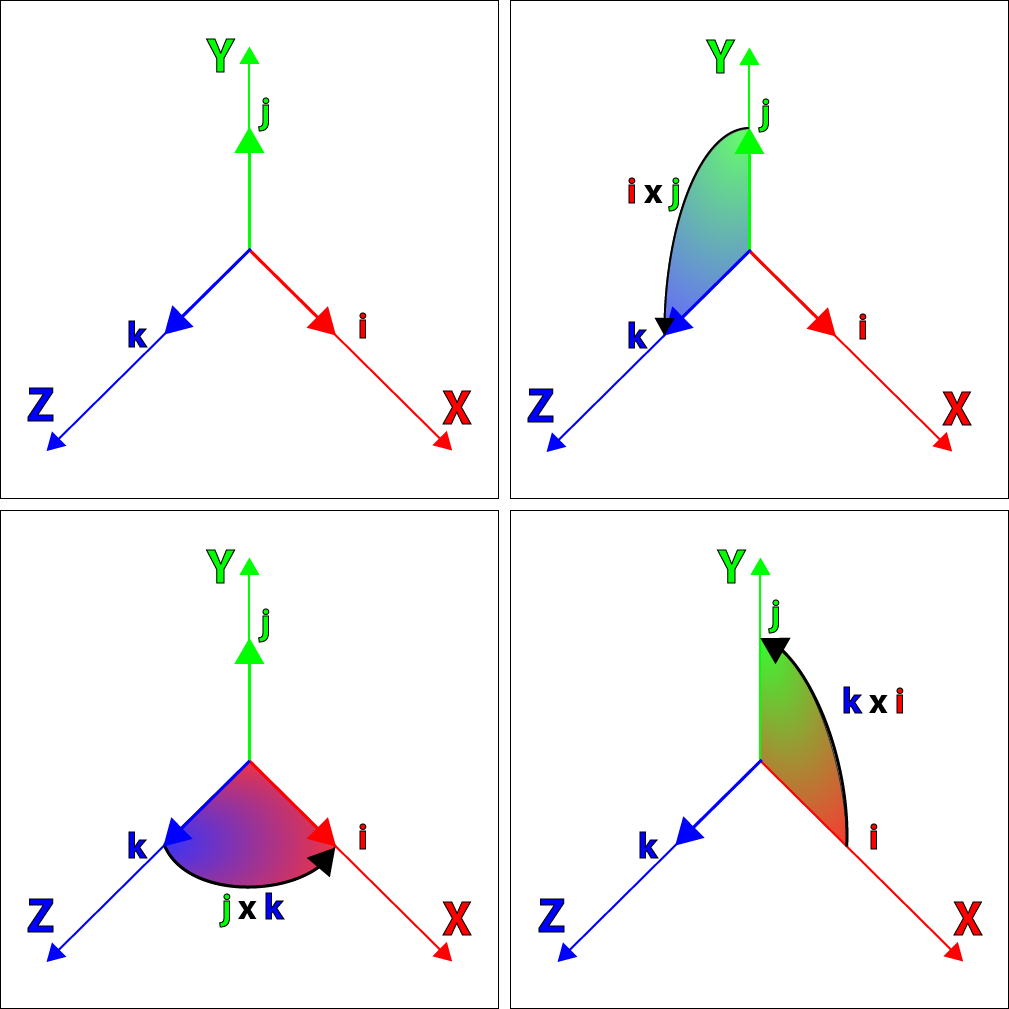
You may have noticed that the relationship between \(i\), \(j\), and \(k\) are very similar to the cross product rules for the unit cartesian vectors:
\[\begin{array}{ccc}\mathbf{x}\times \mathbf{y}=\mathbf{z} & \mathbf{y}\times \mathbf{z}=\mathbf{x} & \mathbf{z}\times \mathbf{x}=\mathbf{y} \\ \mathbf{y}\times \mathbf{x}=-\mathbf{z} & \mathbf{z}\times \mathbf{y}=-\mathbf{x} & \mathbf{x}\times \mathbf{z}=-\mathbf{y}\end{array}\]
Hamilton also recognized that the \(i\), \(j\), and \(k\) imaginary numbers could be used to represent three cartesian unit vectors \(\mathbf{i}\), \(\mathbf{j}\), and \(\mathbf{k}\) with the same properties of imaginary numbers, such that \(\mathbf{i}^2=\mathbf{j}^2=\mathbf{k}^2=-1\).
The image above visualizes the relationship between the cartesian unit vectors represented by \(\mathbf{i}\), \(\mathbf{j}\), and \(\mathbf{k}\).
Quaternions as an Ordered Pair
We can also represent quaternions as an ordered pair:
\[q=[s,\mathbf{v}]~~s\in\mathbb{R}, \mathbf{v}\in\mathbb{R}^3\]
Where \(\mathbf{v}\) can also be represented by its individual components:
\[q=[s,x\mathbf{i}+y\mathbf{j}+z\mathbf{k}]~~s,x,y,z\in\mathbb{R}\]
Using this notation, we can more easily show the similarities between quaternions and complex numbers.
Adding and Subtracting Quaternions
Quaternions can be added and subtracted similar to complex numbers:
\[\begin{array}{rcl}q_a & = & [s_a,\mathbf{a}] \\ q_b & = & [s_b,\mathbf{b}] \\ q_a+q_b & = & [s_a+s_b,\mathbf{a}+\mathbf{b}] \\ q_a-q_b & = & [s_a-s_b,\mathbf{a}-\mathbf{b}]\end{array}\]
Quaternion Products
We can also express the product of two quaternions:
\[\begin{array}{rcl}q_a & = & [s_a,\mathbf{a}] \\ q_b & = & [s_b,\mathbf{b}] \\ q_{a}q_{b} & = & [s_{a},\mathbf{a}][s_{b},\mathbf{b}] \\ & = & (s_{a}+x_{a}i+y_{a}j+z_{a}k)(s_{b}+x_{b}i+y_{b}j+z_{b}k) \\ & = & (s_{a}s_{b}-x_{a}x_{b}-y_{a}y_{b}-z_{a}z_{b}) \\ & & +(s_{a}x_{b}+s_{b}x_{a}+y_{a}z_{b}-y_{b}z_{a})i \\ & & +(s_{a}y_{b}+s_{b}y_{a}+z_{a}x_{b}-z_{b}x_{a})j \\ & & +(s_{a}z_{b}+s_{b}z_{a}+x_{a}y_{b}-x_{b}y_{a})k\end{array}\]
Which results in another quaternion. If we replace the imaginary numbers \(i\), \(j\), and \(k\) in the previous expression by the ordered pairs (also known as the quaternion units),
\[i=[0,\mathbf{i}]~j=[0,\mathbf{j}]~k=[0,\mathbf{k}]\]
And substituting back to the original expression together with \([1,\mathbf{0}]=1\) gives:
\[\begin{array}{rcl}[s_{a},\mathbf{a}][s_{b},\mathbf{b}] & = & (s_{a}s_{b}-x_{a}x_{b}-y_{a}y_{b}-z_{a}z_{b})[1,\mathbf{0}] \\ & & +(s_{a}x_{b}+s_{b}x_{a}+y_{a}z_{b}-y_{b}z_{a})[0,\mathbf{i}] \\ & & +(s_{a}y_{b}+s_{b}y_{a}+z_{a}x_{b}-z_{b}x_{a})[0,\mathbf{j}] \\ & & +(s_{a}z_{b}+s_{b}z_{a}+x_{a}y_{b}-x_{b}y_{a})[0,\mathbf{k}]\end{array}\]
And expanding this expression into a sum of ordered pairs gives:
\[\begin{array}{rcl}[s_{a},\mathbf{a}][s_{b},\mathbf{b}] & = & [s_{a}s_{b}-x_{a}x_{b}-y_{a}y_{b}-z_{a}z_{b},\mathbf{0}] \\ & & +[0,(s_{a}x_{b}+s_{b}x_{a}+y_{a}z_{b}-y_{b}z_{a})\mathbf{i}] \\ & & +[0,(s_{a}y_{b}+s_{b}y_{a}+z_{a}x_{b}-z_{b}x_{a})\mathbf{j}] \\ & & +[0,(s_{a}z_{b}+s_{b}z_{a}+x_{a}y_{b}-x_{b}y_{a})\mathbf{k}]\end{array}\]
If we multiply through with the quaternion unit and extract the common vector components, we can rewrite this equation in this way:
\[\begin{array}{rcl}[s_{a},\mathbf{a}][s_{b},\mathbf{b}] & = & [s_{a}s_{b}-x_{a}x_{b}-y_{a}y_{b}-z_{a}z_{b},\mathbf{0}] \\ & & +[0,s_{a}(x_{b}\mathbf{i}+y_{b}\mathbf{j}+z_{b}\mathbf{k})+s_{b}(x_{a}\mathbf{i}+y_{a}\mathbf{j}+z_{a}\mathbf{k}) \\ & & +(y_{a}z_{b}-y_{b}z_{a})\mathbf{i}+(z_{a}x_{b}-z_{b}x_{a})\mathbf{j}+(x_{a}y_{b}-x_{b}y_{a})\mathbf{k}]\end{array}\]
This equation gives us the sum of two ordered pairs. The first ordered pair is a Real quaternion and the second is a Pure quaternion. These two ordered pairs can be combined into a single ordered pair:
\[\begin{array}{rcl}[s_{a},\mathbf{a}][s_{b},\mathbf{b}] & = & [s_{a}s_{b}-x_{a}x_{b}-y_{a}y_{b}-z_{a}z_{b}, \\ & & s_{a}(x_{b}\mathbf{i}+y_{b}\mathbf{j}+z_{b}\mathbf{k})+s_{b}(x_{a}\mathbf{i}+y_{a}\mathbf{j}+z_{a}\mathbf{k}) \\ & & +(y_{a}z_{b}-y_{b}z_{a})\mathbf{i}+(z_{a}x_{b}-z_{b}x_{a})\mathbf{j}+(x_{a}y_{b}-x_{b}y_{a})\mathbf{k}]\end{array}\]
And if we substitute,
\[\begin{array}{rcl}\mathbf{a} & = & x_{a}\mathbf{i}+y_{a}\mathbf{j}+z_{a}\mathbf{k} \\ \mathbf{b} & = & x_{b}\mathbf{i}+y_{b}\mathbf{j}+z_{b}\mathbf{k} \\ \mathbf{a}\cdot\mathbf{b} & = & x_{a}x_{b}+y_{a}y_{b}+z_{a}z_{b} \\ \mathbf{a}\times\mathbf{b} & = & (y_{a}z_{b}-y_{b}z_{a})\mathbf{i}+(z_{a}x_{b}-z_{b}x_{a})\mathbf{j}+(x_{a}y_{b}-x_{b}y_{a})\mathbf{k}\end{array}\]
We get:
\[[s_{a},\mathbf{a}][s_{b},\mathbf{b}]=[s_{a}s_{b}-\mathbf{a}\cdot\mathbf{b},s_{a}\mathbf{b}+s_{b}\mathbf{a}+\mathbf{a}\times\mathbf{b}]\]
Which is the general equation of a quaternion product.
A Real Quaternion
A Real Quaternion is a quaternion with a vector term of \(\mathbf{0}\):
\[q=[s,\mathbf{0}]\]
And the product of two Real Quaternions is another Real Quaternion:
\[\begin{array}{rcl}q_a & = & [s_a,\mathbf{0}] \\ q_b & = & [s_b,\mathbf{0}] \\ q_{a}q_{b} & = & [s_a,\mathbf{0}][s_b,\mathbf{0}] \\ & = & [s_{a}s_{b},\mathbf{0}]\end{array}\]
Which is similar to the product of two complex numbers that contain a zero imaginary term.
\[\begin{array}{rcl}z_1 & = & a_1+0i \\ z_2 & = & a_2+0i \\ z_{1}z_{2} & = & (a_1+0i)(a_2+0i) \\ & = & a_{1}a_{2}\end{array}\]
Multiplying a Quaternion by a Scalar
We can also multiply a quaternion by a scalar which should obey the rule:
\[\begin{array}{rcl}q & = & [s,\mathbf{v}] \\ \lambda{q} & = & \lambda[s,\mathbf{v}] \\ & = & [\lambda{s},\lambda\mathbf{v}]\end{array}\]
We can confirm this by using the product or Real Quaterions shown above to multiply a quaternion by the scalar as a Real Quaternion:
\[\begin{array}{rcl}q & = & [s,\mathbf{v}] \\ \lambda & = & [\lambda,\mathbf{0}] \\ \lambda{q} & = & [\lambda,\mathbf{0}][s,\mathbf{v}] \\ & = & [\lambda{s},\lambda\mathbf{v}]\end{array}\]
Pure Quaternions
Similar to Real Quaterions, Hamilton also defined the Pure Quaternion as a quaternion that has a zero scalar term:
\[q=[0,\mathbf{v}]\]
Or, written in its component parts:
\[q=xi+yj+zk\]
And we can also take the product of two Pure quaternions:
\[\begin{array}{rcl}q_a & = & [0,\mathbf{a}] \\ q_b & = & [0,\mathbf{b}] \\ q_{a}q_{b} & = & [0,\mathbf{a}][0,\mathbf{b}] \\ & = & [-\mathbf{a}\cdot\mathbf{b},\mathbf{a}\times\mathbf{b}]\end{array}\]
According to the quaternion product rule shown above.
Additive Form of a Quaternion
We can also express quaternions as an addition of the Real and Pure quaternion parts:
\[\begin{array}{rcl}q & = & [s,\mathbf{v}] \\ & = & [s,\mathbf{0}]+[0,\mathbf{v}]\end{array}\]
Unit Quaternion
Given an arbitrary vector \(\mathbf{v}\), we can express this vector in both its scalar magnitude and its direction as such:
\[\mathbf{v}=v\mathbf{\hat{v}}~\text{where}~v=|\mathbf{v}|~\text{and}~|\mathbf{\hat{v}}|=1\]
And combining this definition with the definition of a pure quaternion gives:
\[\begin{array}{rcl}q & = & [0,\mathbf{v}] \\ & = & [0,v\mathbf{\hat{v}}] \\ & = & v[0,\mathbf{\hat{v}}]\end{array}\]
And we can also describe a unit quaternion that has a zero scalar and a unit vector as such:
\[\hat{q}=[0,\mathbf{\hat{v}}]\]
Binary Form of a Quaternion
We can now combine the definitions of the unit quaternion and the additive form of a quaternion, we can create a representation of quaternions which is similar to the notation used to describe complex numbers:
\[\begin{array}{rcl}q & = & [s,\mathbf{v}] \\ & = & [s,\mathbf{0}]+[0,\mathbf{v}] \\ & = & [s,\mathbf{0}]+v[0,\mathbf{\hat{v}}] \\ & = & s+v\hat{q}\end{array}\]
This gives us a way to represent the quaternion that is very similar to complex numbers:
\[\begin{array}{rcl}z & = & a+bi \\ q & = & s + v\hat{q}\end{array}\]
Quaternion Conjugate
The quaternion conjugate can be computed by negating the vector part of the quaternion:
\[\begin{array}{rcl}q & = & [s,\mathbf{v}] \\ q^* & = & [s,-\mathbf{v}]\end{array}\]
And the product of a quaternion with its conjugate gives:
\[\begin{array}{rcl}qq^* & = & [s,\mathbf{v}][s,-\mathbf{v}] \\ & = & [s^2-\mathbf{v}\cdot-\mathbf{v},-s\mathbf{v}+s\mathbf{v}+\mathbf{v}\times-\mathbf{v}] \\ & = & [s^2+\mathbf{v}\cdot\mathbf{v},\mathbf{0}] \\ & = & [s^2+v^2,\mathbf{0}]\end{array}\]
Quaternion Norm
If you recall from the definition of the norm of a complex number:
\[\begin{array}{rcl}|z| & = & \sqrt{a^2+b^2} \\ zz^* & = & |z|^2\end{array}\]
Similarly, the norm (or magnitude) of a quaternion is defined as:
\[\begin{array}{rcl}q & = & [s,\mathbf{v}] \\ |q| & = & \sqrt{s^2+v^2}\end{array}\]
Which allows us to express the norm of a quaternion as:
\[qq^*=|q|^2\]
Quaternion Normalization
With the definition of a quaternion norm, we can use it to normalize a quaternion. A quaternion is normalized by dividing it by \(|q|\):
\[q^{\prime}=\frac{q}{\sqrt{s^2+v^2}}\]
As an example, let’s normalize the quaternion:
\[q=[1,4\mathbf{i}+4\mathbf{j}-4\mathbf{k}]\]
First, we must compute the norm of the quaternion:
\[\begin{array}{rcl}|q| & = & \sqrt{1^2+4^2+4^2+(-4)^2} \\ & = & \sqrt{49} \\ & = & 7\end{array}\]
Then, we must divide the quaternion by the norm of the quaternion to compute the normalized quaternion:
\[\begin{array}{rcl}q^{\prime} & = & \cfrac{q}{|q|} \\[1.0em] & = & \cfrac{(1+4\mathbf{i}+4\mathbf{j}-4\mathbf{k})}{7} \\[1.0em] & = & \cfrac{1}{7}+\cfrac{4}{7}\mathbf{i}+\cfrac{4}{7}\mathbf{j}-\cfrac{4}{7}\mathbf{k}\end{array}\]
Quaternion Inverse
The inverse of a quaternion is denoted \(q^{-1}\). To compute the inverse of a quaternion, we take the conjugate of the quaternion and divide it by the square of the norm:
\[q^{-1}=\frac{q^*}{|q|^2}\]
To show this, we can take the fact that by definition of the inverse:
\[qq^{-1}=[1,\mathbf{0}]=1\]
And multiply both sides by the conjugate of the quaternion gives:
\[q^{*}qq^{-1}=q^{*}\]
And by substitution we get:
\[\begin{array}{rcl}|q|^{2}q^{-1} & = & q^{*} \\ q^{-1} & = & \cfrac{q^{*}}{|q|^{2}}\end{array}\]
And for unit-norm quaternions whose norm is 1, we can write:
\[q^{-1}=q^{*}\]
Quaternion Dot Product
Similar to vector dot-products, we can also compute the dot product between two quaternions by multiplying the corresponding scalar parts and summing the results:
\[\begin{array}{rcl}q_1 & = & [s_1,x_1\mathbf{i}+y_1\mathbf{j}+z_1\mathbf{k}] \\ q_2 & = & [s_2,x_2\mathbf{i}+y_2\mathbf{j}+z_2\mathbf{k}] \\ q_1{\cdot}q_2 & = & s_{1}s_{2}+x_{1}x_{2}+y_{1}y_{2}+z_{1}z_{2}\end{array}\]
We can also use the quaternion dot-product to compute the angular difference between the quaternions:
\[\cos\theta=\frac{s_{1}s_{2}+x_{1}x_{2}+y_{1}y_{2}+z_{1}z_{2}}{|q_{1}||q_{2}|}\]
And for unit-norm quaternions, we can simplify the equation:
\[\cos\theta=s_{1}s_{2}+x_{1}x_{2}+y_{1}y_{2}+z_{1}z_{2}\]
Rotations
If you recall we defined a special form of the complex number called a Rotor that could be used to rotate a point through the 2D complex plane as:
\[q=\cos\theta+i\sin\theta\]
Then by its similarities to complex numbers, it should be possible to express a quaternion that can be used to rotate a point in 3D-space as such:
\[q=[\cos\theta,\sin\theta\mathbf{v}]\]
Let’s test if this theory holds by computing the product of the quaternion \(q\) and the vector \(\mathbf{p}\). First, we can express \(\mathbf{p}\) as a Pure quaternion in the form:
\[p=[0,\mathbf{p}]\]
And \(q\) is a unit-norm quaternion in the form:
\[q=[s,\lambda\mathbf{\hat{v}}]\]
Then,
\[\begin{array}{rcl}p^{\prime} & = & qp \\ & = & [s,\lambda\mathbf{\hat{v}}][0,\mathbf{p}] \\ & = & [-\lambda\mathbf{\hat{v}}\cdot\mathbf{p},s\mathbf{p}+\lambda\mathbf{\hat{v}}\times\mathbf{p}]\end{array}\]
We see that the result is a general quaternion with both scalar and a vector parts.
Let’s first consider the “special” case where \(\mathbf{p}\) is perpendicular to \(\mathbf{\hat{v}}\) in which case, the dot-product term \(-\lambda\mathbf{\hat{v}}\cdot\mathbf{p}=0\) and the result becomes the Pure quaternion:
\[p^{\prime}=[0,s\mathbf{p}+\lambda\mathbf{\hat{v}}\times\mathbf{p}]\]
In this case, to rotate \(\mathbf{p}\) about \(\mathbf{\hat{v}}\) we just substitute \(s=\cos\theta\) and \(\lambda=\sin\theta\).
\[p^{\prime}=[0,\cos\theta\mathbf{p}+\sin\theta\mathbf{\hat{v}}\times\mathbf{p}]\]
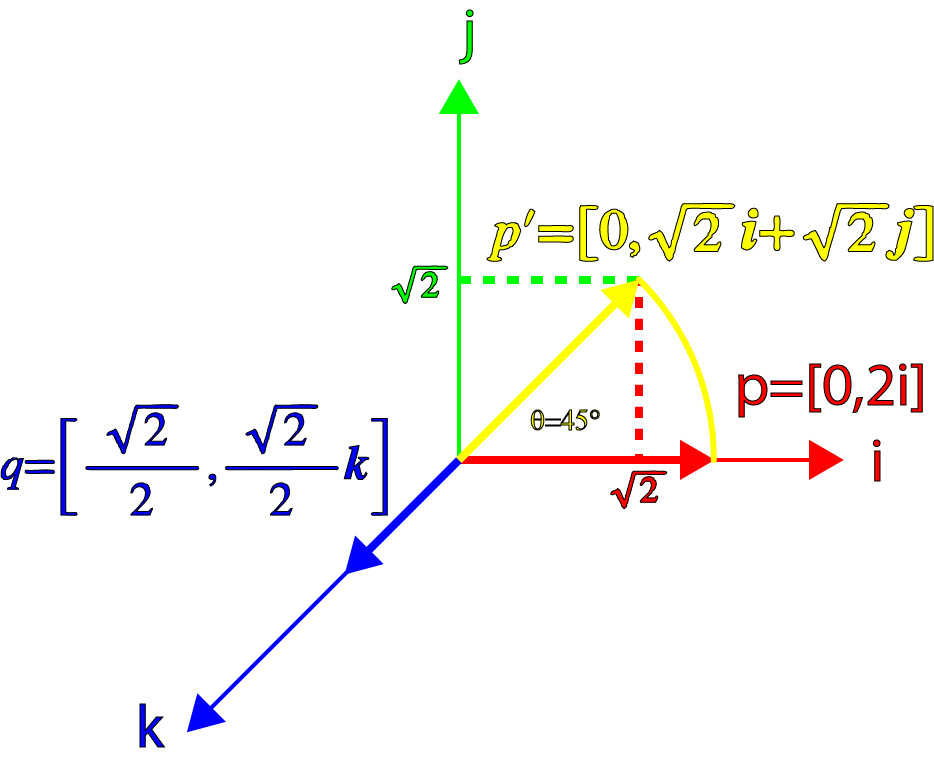
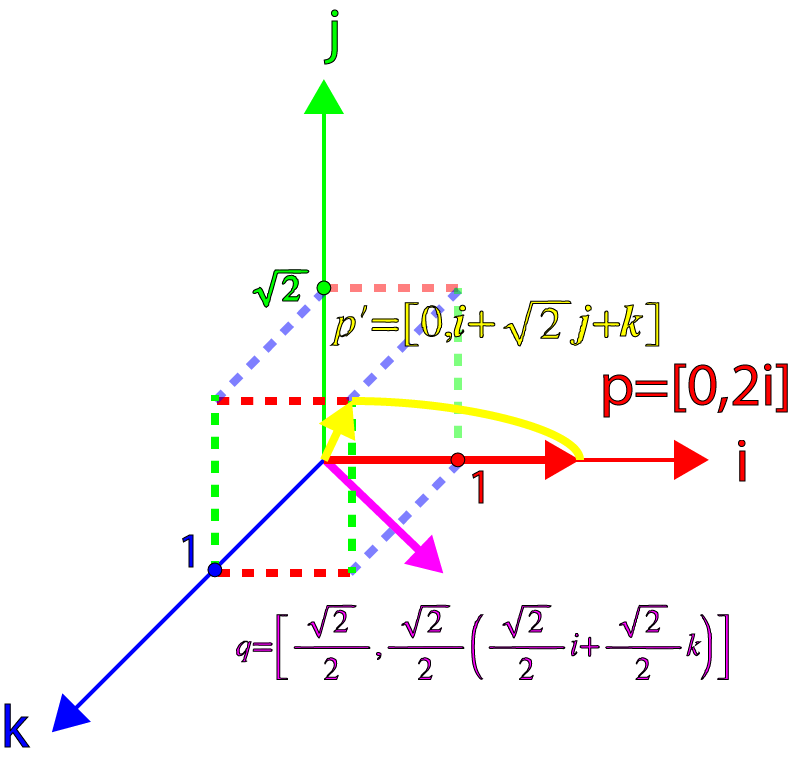
As an example, let’s rotate a vector \(\mathbf{p}\) 45° about the z-axis then our quaternion \(q\) is:
\[\begin{array}{rcl}q & = & [\cos\theta,\sin\theta\mathbf{k}] \\ & = & \left[\frac{\sqrt{2}}{2},\frac{\sqrt{2}}{2}\mathbf{k}\right]\end{array}\]
And let’s take a vector \(\mathbf{p}\) that adheres to the special case that \(\mathbf{p}\) is perpendicular to \(\mathbf{k}\):
\[p=[0,2\mathbf{i}]\]
Now let’s find the product of \(qp\):
\[\begin{array}{rcl}p^{\prime} & = & qp \\ & = & \left[\frac{\sqrt{2}}{2},\frac{\sqrt{2}}{2}\mathbf{k}\right][0,2\mathbf{i}] \\ & = & \left[0,2\frac{\sqrt{2}}{2}\mathbf{i}+2\frac{\sqrt{2}}{2}\mathbf{k}\times\mathbf{i}\right] \\ & = & [0, \sqrt{2}\mathbf{i}+\sqrt{2}\mathbf{j}]\end{array}\]
Which results in a Pure quaternion that is rotated 45° about the \(\mathbf{k}\) axis. We can also confirm that the magnitude of the resulting vector is maintained:
\[\begin{array}{rcl}|\mathbf{p}^{\prime}| & = & \sqrt{\sqrt{2}^{2}+\sqrt{2}^{2}} \\ & = & 2\end{array}\]
Which is exactly the result we expected!
We can visualize this by the following image:
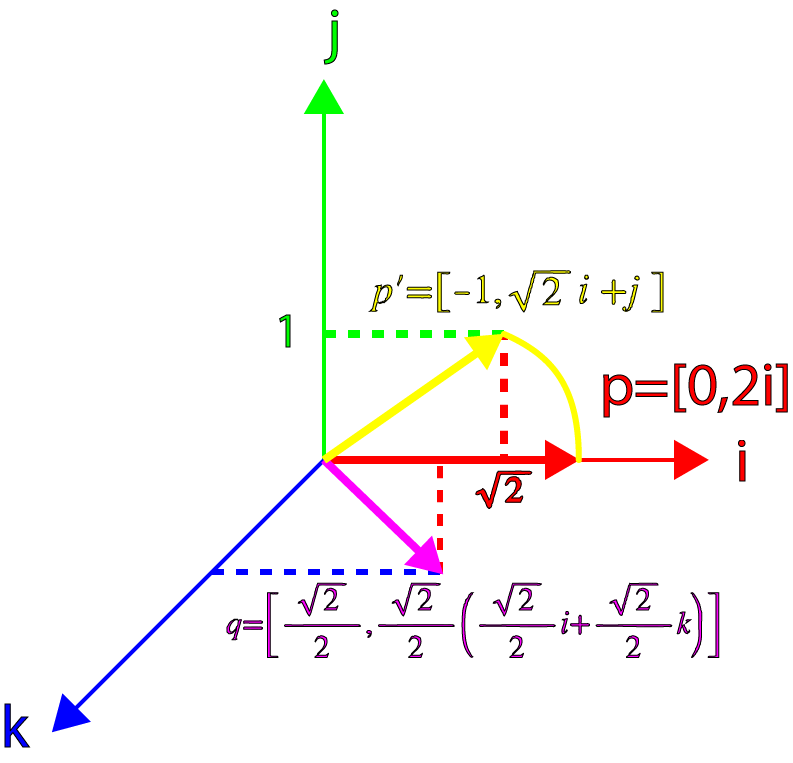
Now let’s consider a quaternion that is not orthogonal to \(\mathbf{p}\). If we specify the vector part of our quaternion to 45° offset from \(\mathbf{p}\) we get:
\[\begin{array}{rcl}\mathbf{\hat{v}} & = & \frac{\sqrt{2}}{2}\mathbf{i}+\frac{\sqrt{2}}{2}\mathbf{k} \\ \mathbf{p} & = & 2\mathbf{i} \\ q & = & [\cos\theta,\sin\theta\mathbf{\hat{v}}] \\ p & = & [0,\mathbf{p}]\end{array}\]
And multiplying our vector \(\mathbf{p}\) by \(q\) we get:
\[\begin{array}{rcl}p^{\prime} & = & qp \\ & = & [\cos\theta,sin\theta\mathbf{\hat{v}}][0,\mathbf{p}] \\ & = & [-\sin\theta\mathbf{\hat{v}}\cdot\mathbf{p},\cos\theta\mathbf{p}+\sin\theta\mathbf{\hat{v}}\times\mathbf{p}]\end{array}\]
And substituting \(\mathbf{\hat{v}}\), \(\mathbf{p}\) and \(\theta=45^{\circ}\) gives:
\[\begin{array}{rcl}p^{\prime} & = & \left[-\frac{\sqrt{2}}{2}\left(\frac{\sqrt{2}}{2}\mathbf{i}+\frac{\sqrt{2}}{2}\mathbf{k}\right)\cdot(2\mathbf{i}),\frac{\sqrt{2}}{2}2\mathbf{i}+\frac{\sqrt{2}}{2}\left(\frac{\sqrt{2}}{2}\mathbf{i}+\frac{\sqrt{2}}{2}\mathbf{k}\right)\times2\mathbf{i}\right] \\ & = & [-1,\sqrt{2}\mathbf{i}+\mathbf{j}]\end{array}\]
Which is no longer a pure quaternion, and it has not been rotated 45° and the vector’s norm is no longer 2 (instead it has been reduced to \(\sqrt{3}\)).
This result can be visualized by the image.
However, all is not lost. Hamilton recognized (but didn’t publish) that if we post-multiply the result of \(qp\) by the inverse of \(q\) then the result is a pure quaternion and the norm of the vector component is maintained. Let’s see if we can apply this to our example.
First, let’s compute \(q^{-1}\):
\[\begin{array}{rcl}q & = & \left[\cos\theta,\sin\theta\left(\frac{\sqrt{2}}{2}\mathbf{i}+\frac{\sqrt{2}}{2}\mathbf{k}\right)\right] \\ q^{-1} & = & \left[\cos\theta,-\sin\theta\left(\frac{\sqrt{2}}{2}\mathbf{i}+\frac{\sqrt{2}}{2}\mathbf{k}\right)\right]\end{array}\]
For \(\theta=45^{\circ}\) gives:
\[\begin{array}{rcl}q^{-1} & = & \left[\frac{\sqrt{2}}{2},-\frac{\sqrt{2}}{2}\left(\frac{\sqrt{2}}{2}\mathbf{i}+\frac{\sqrt{2}}{2}\mathbf{k}\right)\right] \\ & = & \frac{1}{2}\left[\sqrt{2},-\mathbf{i}-\mathbf{k}\right]\end{array}\]
And combining the previous value of \(qp\) and \(q^{-1}\) gives:
\[\begin{array}{rcl}qp & = & \left[-1,\sqrt{2}\mathbf{i}+\mathbf{j}\right] \\ qpq^{-1} & = & \left[-1,\sqrt{2}\mathbf{i}+\mathbf{j}\right]\frac{1}{2}\left[\sqrt{2},-\mathbf{i}-\mathbf{k}\right] \\ & = & \frac{1}{2}\left[-\sqrt{2}-\left(\sqrt{2}\mathbf{i}+\mathbf{j}\right)\cdot(-\mathbf{i}-\mathbf{k}),\mathbf{i}+\mathbf{k}+\sqrt{2}\left(\sqrt{2}\mathbf{i}+\mathbf{j}\right)-\mathbf{i}+\sqrt{2}\mathbf{j}+\mathbf{k}\right] \\ & = & \frac{1}{2}\left[-\sqrt{2}+\sqrt{2},\mathbf{i}+\mathbf{k}+2\mathbf{i}+\sqrt{2}\mathbf{j}-\mathbf{i}+\sqrt{2}\mathbf{j}+\mathbf{k}\right] \\ & = & \left[0,\mathbf{i}+\sqrt{2}\mathbf{j}+\mathbf{k}\right]\end{array}\]
Which is a pure quaternion and the norm of the result is:
\[\begin{array}{rcl}|p^{\prime}| & = & \sqrt{1^2+\sqrt{2}^2+1^2} \\ & = & \sqrt{4} \\ & = & 2\end{array}\]
which is the same as \(\mathbf{p}\) so the norm of the vector is maintained.
The image below visualizes the result of the rotation.
So we can see that the result is a pure quaternion and that the norm of the initial vector is maintained, but the vector has been rotated 90° rather than 45° which is twice as much as desired! So in order to correctly rotate a vector \(\mathbf{p}\) by an angle \(\theta\) about an arbitrary axis \(\mathbf{\hat{v}}\), we must consider the half-angle and construct the following quaternion:
\[q=\left[\cos\frac{1}{2}\theta,\sin\frac{1}{2}\theta\mathbf{\hat{v}}\right]\]
Which is the general form of a rotation quaternion!
Quaternion Interpolation
One of the most important reasons for using quaternions in computer graphics is that quaternions are very good at representing rotations in space. Quaternions overcome the issues that plague other methods of rotating points in 3D space such as Gimbal lock which is an issue when you represent your rotation with euler angles.
Using quaternions, we can define several methods that represents a rotational interpolation in 3D space. The first method I will examine is called SLERP which is used to smoothly interpolate a point between two orientations. The second method is an extension of SLERP called SQAD which is used to interpolate through a sequence of orientations that define a path.
SLERP
SLERP stands for Spherical Linear Interpolation. SLERP provides a method to smoothly interpolate a point about two orientations.
I will represent the first orientation as \(q_1\) and the second orientation as \(q_2\). The point that is interpolated will be represented by \(\mathbf{p}\) and the interpolated point will be represented by \(\mathbf{p}^{\prime}\). The interpolation parameter \(t\) will interpolate \(\mathbf{p}\) from \(q_1\) when \(t=0\) to \(q_2\) when \(t=1\).
The standard linear interpolation formula is:
\[\mathbf{p}^{\prime}=\mathbf{p_1}+t(\mathbf{p_2}-\mathbf{p_1})\]
The general steps to apply this equation are:
- Compute the difference between \(\mathbf{p_1}\) and \(\mathbf{p_2}\).
- Take the fractional part of that difference.
- Adjust the original value by the fractional difference between the two points.
We can use the same basic principle to interpolate between two quaternion orientations.
Quaternion Difference
The first step dictates that we must compute the difference between \(q_1\) and \(q_2\). With regards to quaternions, this is equivalent to computing the angular difference between the two quaternions.
\[\Delta{q}=q_1^{-1}q_2\]
Quaternion Exponentiation
The next step is to take the fractional part of that difference. We can compute the fractional part of a quaternion by raising it to a power whose value is in the range \([0…1]\).
The general formula for quaternion exponentiation is:
\[q^t=\exp(t\log{q})\]
Where the exponential function for quaternions is given by:
\[\begin{array}{rcl}\exp(q) & = & \exp\left([0,\theta\mathbf{\hat{v}}]\right) \\ & = & [\cos\theta,\sin\theta\mathbf{\hat{v}}] \end{array}\]
And the logarithm of a quaternion is given by:
\[\begin{array}{rcl}\log{q} & = & \log(\cos\theta{+}\sin\theta\mathbf{\hat{v}}) \\ & = & \log\left(\exp(\theta\mathbf{\hat{v}})\right) \\ & = & \theta\mathbf{\hat{v}} \\ & = & [0,\theta\mathbf{\hat{v}}] \end{array}\]
For \(t=0\), we have:
\[\begin{array}{rcl}q^0 & = & \exp(0\log{q}) \\ & = & \exp([\cos(0),\sin(0)\mathbf{\hat{v}}]) \\ & = & \exp([1,\mathbf{0}]) \\ & = & [1,\mathbf{0}]\end{array}\]
And for \(t=1\), we have:
\[\begin{array}{rcl}q^1 & = & \exp(\log{q}) \\ & = & q\end{array}\]
Fractional Difference of Quaternions
To compute the interpolated angular rotation, we adjust the original orientation \(q_1\) by the fractional part of the difference between \(q_1\) and \(q_2\).
\[q^{\prime}=q_1\left(q_1^{-1}q_2\right)^t\]
Which is the general form of spherical linear interpolation using quaternions. However, this is not the form of the SLERP equation that is commonly used in practice.
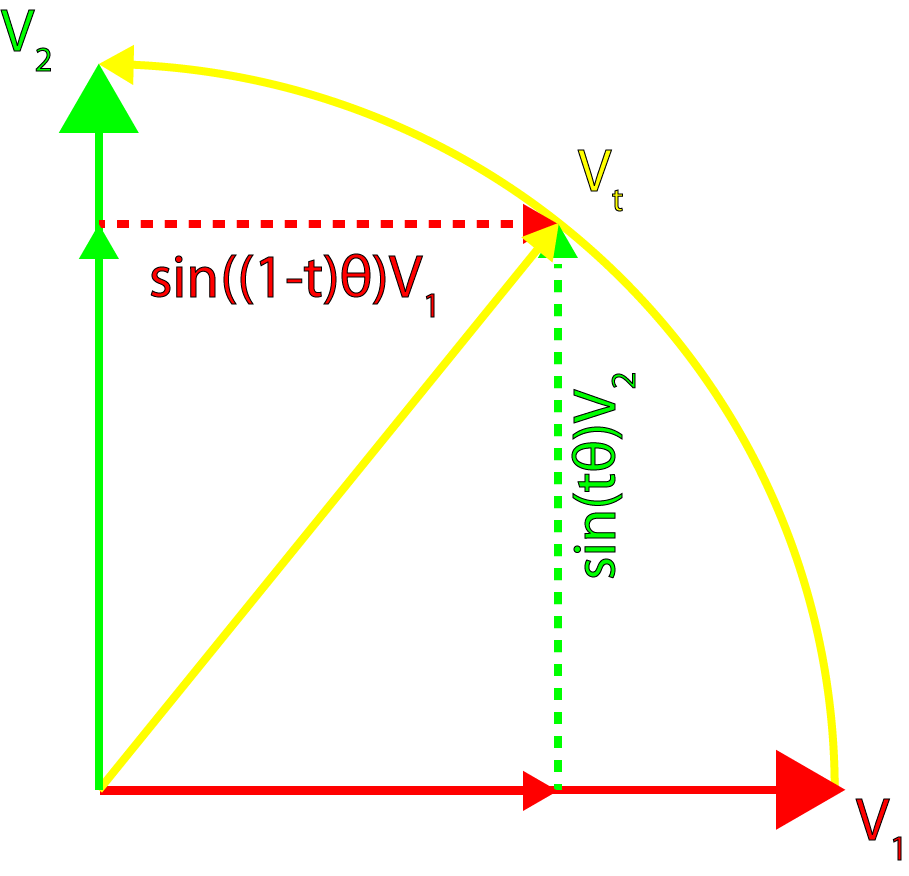
We can apply a similar formula for performing a spherical interpolation of vectors to quaternions. The general form of a spherical interpolation for vectors is defined as:
\[\mathbf{v}_t=\frac{\sin(1-t)\theta}{\sin\theta}\mathbf{v}_1+\frac{\sin{t\theta}}{\sin\theta}\mathbf{v}_2\]
This is visualized in the following image.
This formula can be applied unmodified to quaternions:
\[q_t=\frac{\sin(1-t)\theta}{\sin\theta}q_1+\frac{\sin{t\theta}}{\sin\theta}q_2\]
And we can obtain the angle \(\theta\) by computing the dot-product between \(q_1\) and \(q_2\).
\[\begin{array}{rcl}\cos\theta & = & \cfrac{q_1{\cdot} q_2}{|q_1||q_2|} \\ & = & \cfrac{s_{1}s_{2}+x_{1}x_{2}+y_{1}y_{2}+z_{1}z_{2}}{|q_1||q_2|} \\ \theta & = & \cos^{-1}\left(\cfrac{s_{1}s_{2}+x_{1}x_{2}+y_{1}y_{2}+z_{1}z_{2}}{|q_1||q_2|}\right)\end{array}\]
Considerations
There are two issues with this implementation which must be taken into consideration during implementation.
First, if the quaternion dot-product results in a negative value, then the resulting interpolation will travel the “long-way” around the 4D sphere which is not necessarily what we want. To solve this problem, we can test the result of the dot product and if it is negative, then we can negate one of the orientations. Negating the scalar and the vector part of the quaternion does not change the orientation that it represents but by doing this we guarantee that the rotation will be applied in the “shortest” path.
The other problem arises when the angular difference between \(q_1\) and \(q_2\) is very small then \(\sin\theta\) becomes 0. If this happens, then we will get an undefined result when we divide by \(\sin\theta\). In this case, we can fall-back to using linear interpolation between \(q_1\) and \(q_2\).
SQUAD
Just as a SLERP can be used to compute an interpolation between two quaternions, a SQUAD (Spherical and Quadrangle) can be used to smoothly interpolate over a path of rotations.
If we have the sequence of quaternions:
\[q_1,q_2,q_3,\cdots,q_{n-2},q_{n-1},q_{n}\]
And we also define the “helper” quaternion (\(s_i\)) which we can consider an intermediate control point:
\[s_i=\exp\left(-\frac{\log\left(q_{i+1}q_i^{-1}\right)+\log\left(q_{i-1}q_i^{-1}\right)}{4}\right)q_i\]
Then the orientation along the sub-cuve defined by:
\[q_{i-1},q_i,q_{i+1},q_{i+2}\]
at time t is given by:
\[\mathrm{squad}(q_i,q_{i+1},s_i,s_{i+1},t)=\mathrm{slerp}(\mathrm{slerp}(q_i,q_{i+1},t),\mathrm{slerp}(s_i,s_{i+1},t),2t(1-t))\]
Conclusion
Despite being extremely difficult to understand, quaternions provide a few obvious advantages over using matrices or Euler angles for representing rotations.
- Quaternion interpolation using SLERP and SQUAD provide a way to interpolate smoothly between orientations in space.
- Rotation concatenation using quaternions is faster than combining rotations expressed in matrix form.
- For unit-norm quaternions, the inverse of the rotation is taken by subtracting the vector part of the quaternion. Computing the inverse of a rotation matrix is considerably slower if the matrix is not orthonormalized (if it is, then it’s just the transpose of the matrix).
- Converting quaternions to matrices is slightly faster than for Euler angles.
- Quaternions only require 4 numbers (3 if they are normalized. The Real part can be computed at run-time) to represent a rotation where a matrix requires at least 9 values.
However for all of the advantages in favor of using quaternions, there are also a few disadvantages.
- Quaternions can become invalid because of floating-point round-off error however this “error creep” can be resolved by re-normalizing the quaternion.
- And probably the most significant deterrent for using quaternions is that they are very hard to understand. I hope that this issue is resolved after reading this article.
There are several math libraries that implement quaternions and a few of those libraries implement quaternions correctly. In my personal experience, I find GLM (OpenGL Math Library) to be a good math library with a good implementation of quaternions. If you are interested in using quaternions in your own applications, this is the library I would recommend.
Download the Demo
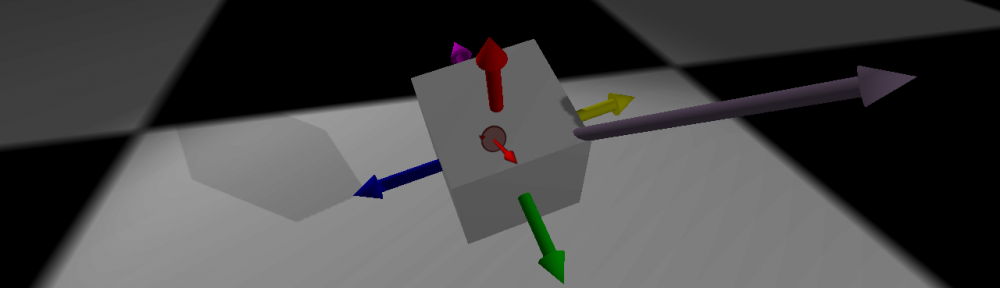
I created a small demo that demonstrates how a quaternion is used to rotate an object in space. The demo was created with Unity 3.5.2 which you can download for free and view the demo script files. The zip file also contains a Windows binary executable but Using Unity, you can also generate a Mac application (and Unity 4 introduces Linux builds as well).
Reference
| Vince, J (2011). Quaternions for Computer Graphics. 1st. ed. London: Springer. | |
| Dunn, F. and Parberry, I. (2002). 3D Math Primer for Graphics and Game Development. 1st. ed. Plano, Texas: Wordware Publishing, Inc. | |
| Quaternions – Wikipedia | |
| Quaternions and Spatial Rotation – Wikipedia |


I like this website.
Thanks Lawrence, you comments are welcome.
so do i
This is a wonderfully clear and concise introduction to quaternions! There are a few typos that could be corrected. “It’s” should be “its” throughout. (The first is a contraction of “it is”, the second is the possessive form of “it”.) Also, “gimble’ should be “gimbal”. And “principal” should be “principle”: both are words but they have different meanings.
I will show this tutorial to all my robotics students.
Dave,
Thanks for the corrections! Let me know if you find anything else.
“Besides being extremely difficult to understand”
would make more sense as:
“Despite being extremely difficult to understand”
Dan,
Thanks for your feedback. I have made the change.
Well done! I find this website through google and found it very informative and useful. I would like to learn graphics programming for a long time, but it’s quite difficult to get started, especially the mathematics, may you kindly suggest what mathematics I should know and how to learn graphics programming effectively? Thank you very much.
Gary,
For basic graphics programming you will want to have a good understanding of vector algebra (vector addition & subtraction, dot & cross products) as well as matrix algebra (matrix products, inverse & transpose). Also knowledge of basic lighting equations is important.
I recommend you read the books I’ve referenced in the math articles here: http://3dgep.com/?cat=27 as well as read the the OpenGL articles here http://3dgep.com/?cat=11.
If you’d like to get into shader programming, then you should follow the Cg articles here: http://3dgep.com/?cat=108.
I also plan to make a set of GLSL articles, but I can’t promise when they will be ready.
Thank you for writing such a thorough post on quaternions, it is much appreciated!
Unfortunately though, quite a few of the equation listings don’t show properly in neither Firefox nor Chrome on my Win7 computer ( see http://grab.by/hQJm for example). Just wanted to let you know 🙂
Thanks for pointing this out. A few weeks after creating this tutorial, the LaTeX generator I was using went offline and i had to switch to another provider. This provider seems to have a different parser than the one I was using when I created the page on quaternions in the first place. I switched again and some of the formulas that were not showing up before are fixed now but others are broken. I really need to install my own CGI handler for LaTex on my own server.
Thanks for the heads-up!
I find this to be a great tutorial but I’m having the same problem Trond had with every single equation, but the way it looks it seems to be a great tutorial.
Luke,
I have moved the script that is used to generate the formulas to a new server. There have been some hiccups with this script but I hope to have them all fixed now.
What happen for some picture of equation.
Henry, when I created this article I was using a different source for the LaTeX generation. That source has since become unavailable so I had to switch to another source which apparently handles LaTeX differently. I need to go through each equation which isn’t rendering correctly to find out why this is happening but this takes time… It will be fixed in the future.
This is the only coherent introduction to quaternions I have found on the web. It is failry complex and I will have to read through this several times. I am assuming you are drawing heavily from Vince, as Dunn is pretty sketchy. Thanks for pulling this together–I feel like I have found a startting point!
Excellent tutorial/article on quaternions, it helped me get a good insight, thanks for the effort and this website is great!
While familiar with the use of rotational matrices all my previous attempts to get a hold of quaternions have failed.
What worked for me with your explanation is that you explained it by analogy to rotation in the complex plane which I already understood: the next step was then easy for me.
Many thanks for your work and making it available.
Great tutorial, loving it so far!
I’ve spot one minor error I think though:
> The interpolation parameter t will interpolate P from q1 when t = 0 to q1 when t = 1.
Shouldn’t this be:
> The interpolation parameter t will interpolate P from q1 when t = 0 to q2 when t = 1.
Shammah,
Thanks for pointing this out!
WOW! Very nice article. I actually implemented a simple quaternion library in C++ while reading it :). Very well presented too.
Please it look like very importent&impresive post, but you aware that we can’t read it becouse lack of picture? equations?
Can you attach or sent a full pdf format to read it please?
Mica,
Sorry if the formulas did not show up for you. The images for the formulas are generated on another sever than where the article itself is hosted. If the server that generates the images is inaccessible, then the formulas may not show up. This is annoying but if the images don’t show up, then check back in a few minutes and perhaps it is fixed at that time. I strive for 100% up-time, but some downtime is unavoidable.
The images are ok, but the math markup isn’t rendering. Can this be fixed? There’s a lot of really useful info here, but without the equations rendering properly it’s very difficult to read.
David: The formulas on this page are rendered by your browser using a JavaScript library called MathJax. If the formulas are not rendering for you, it is probably because you have disabled JavaScript in your browser.
To see if the formulas should render, try the demos on the MathJax website: https://www.mathjax.org/#demo.
Thanks, this is actually really relevant to MA2 for first year students aswell.
This was fantastic! Thank you so much for writing it up.
This is a great explanation but I got really stuck at why the product of two quaternions is minus the dot product. We have:
SaSb – XaXb – YaYb – ZaZb, then we substitute in that a.b = XaXbi^2 etc. Does this i^2 (i squared) not resolve to -1 as per Hamilton? That would make a.b equal to -XaXb – YaYb – ZaZb already and it wouldn’t need further negation. I’m obviously missing something in the notation, perhaps that i^2 here is the cosine of 0 and therefore equals 1. Confused!
Gaz,
You are right about the fact that [math]\mathbf{i}^2=\mathbf{j}^2=\mathbf{k}^2=-1[/math] as is stated in the section titled Quaternions.
Maybe if I write the product rule like this:
And we can write the dot product of the vector parts of the two quaternions as:
Which we can substitute back into the original equation:
So we are not adding any extra negatives, we are just factoring out the [math]\mathbf{i}^2=\mathbf{j}^2=\mathbf{k}^2=-1[/math] from the dot-product to get the real part of the quaternion product.
Does this make it more clear?
No, Gaz is right! The squared terms of i, j, and k should be left out of the dot product equation of a dot b. Then it makes sense. As others have said, the best explanation of quaternions that I have seen.
John,
Agreed. I have update the article and removed the squared terms of i, j, and k.
Thanks!
This explanation is still not right. The dot product of a and b is xaxb + yayb + zazb not minus 1 times this result. The algebraic result of squaring i, j and k to yield -1 gives us -a.b which is what needs to substitute the original algebraic expression. There is some confusion in quaternion theory over when to treat i, j and k as imaginary numbers and when to treat them as unit vectors in the Cartesian system.
Stephen,
Doh, you are right! I was treating [math]\mathbf{i}[/math], [math]\mathbf{j}[/math], and [math]\mathbf{k}[/math] as imaginary numbers but in the equation they are unit vectors! I was so blind to this for so long and I couldn’t understand where the confusion was.
Thanks for pointing this out. I have updated the article.
This is a great tutoria, but I think Gaz was onto something as I think the dot product is incorrectly defined and is then substituted into the equations incorrectly i.e. leading to two wrongs make a right!.
In teh abovbve, comment, surely after ‘And we can write the dot product of the vector parts of the two quaternions as:’ is incorrect. the dot product is surely a.b = xaxb + yayb +zazb (by definition) and so xaxbi^2 + yaybj^2 +zazbk^2 = -xaxb – yayb – zazb = – a.b and then ‘Which we can substitute back into the original equation:’ follows and is correct.
So in the main text, after ‘And if we substitute,’ it should be stated that a.b = xaxb + yayb +zazb and NOT a.b = xaxbi^2 + yaybj^2 +zazbk^2, then the rest follows.
Thanks once again for great article.
Mark
Mark,
Thanks for pointing this out. After reading stephen’s comment on March 9, 2016 (here) I realized my mistake. I was treating [math]\mathbf{i}[/math], [math]\mathbf{j}[/math], and [math]\mathbf{k}[/math] as imaginary numbers but they are actually unit vectors.
I have fixed the article with this change.
Ok. I understand why it is SaSb – a.b. But your explain is not true. In here, we represent vector a and b in bases(i, j, k). Therefore a=(xa, ya, za), b=(xb, yb, zb) and dot product a.b=xaxb + yayb + zazb. This is the reason why we need minus before a.b
I’m not sure what part of the explanation is not true? The original equation for the real part is:
[math]s_{a}s_{b}-x_{a}x_{b}-y_{a}y_{b}-z_{a}z_{b}[/math]
If you factor out a [math]-1[/math] from the vector part you get:
[math]s_{a}s_{b}+-1\(x_{a}x_{b}+y_{a}y_{b}+z_{a}z_{b}\)[/math]
Which can be rewritten as:
[math]s_{a}s_{b}-\mathbf{a}\cdot\mathbf{b}[/math]
Is this clear?
Where it says:
“The set of complex numbers (represented by the symbol ) is the sum of a real number and an imaginary number and has the form:”, the following formula is wrong. It should say: z = a + bi; a, b \in R; i^2 = -1, but it does not.
Oskar,
Yes, you are right. Thanks for pointing this out. After switching to a different LaTeX generator some formulas didn’t render correctly anymore. I hope I have fixed all of the places (in this page) where formulas were not rendered correctly anymore but if you seen any more then please let me know!
… and in the following formulas, about addition, subtraction and multiplication, you should not use an implication arrow, you should use an equals sign.
Oskar,
Yes, again you are correct. I can’t remember why I had an implication arrow there but it’s fixed now.
Thanks, this was really useful. I finally understood quaternions. I’ll use them in 3D reconstruction from multiple photos.
Thanks for the article. Found an error in the formulas after: “Complex numbers can also be multiplied by applying normal algebraic rules.”
In row three there stand a2a2 where it should be a1a2.
Bye
Henning,
Thanks for pointing this out. I have fixed the article now.
This article it’s just beautiful. Thank you.
beautiful article.
I suggest you try mathjax.js for equation generation. It`s client-based. no need for host or anything.
i have a doubt. when u calculate the norms int the example, u said, instead of 2 its is root(3). but how is it?? sqrt(1 + 2 + 1) = srt(4) = 2 ???
Akash,
In the example we are rotating the vector [math]\mathbf{p}=2\mathbf{i}[/math] 45° by the quaternion [math]q=[\cos\theta,\sin\theta\mathbf{k}][/math] but in order to perform this operation, we must express [math]\mathbf{p}[/math] as a pure quaternion in the form [math]p=[0,\mathbf{p}][/math]. (notice how vectors are expressed use bold-face characters and quaternions are expressed as normal (not bold) characters).
If the quaternion [math]q[/math] correctly rotated the vector [math]\mathbf{p}[/math] then the result should also be a pure quaternion (with no scalar part) and the magnitude of the vector part should be the same as the original vector (because a rotation should not scale the original vector) however this example shows that this is not the case.
The magnitude of the original vector is
But the magnitude of the vector part of the resulting quaternion is:
Which is not the same magnitude as the original vector.
If I wanted to compute the magnitude of the resulting quaternion then I would need to consider the quaternion’s scalar part according to the formula described in the section titled Quaternion Norm. But since I’m only interested in rotating a vector by a quaternion I only want to consider the result of the vector part (and thus discard the scalar part when I compute the magnitude of the resulting vector).
I hope this answers your question.
and I have a question.what
s that suppose to mean?if a+bi is a point,isnt that a Matrix multipy a point equals to a point more correct?
cubase01,
Sorry, the matrix representation of a complex number is not explained in this article. I will try to briefly explain it here.
We can represent a complex number as the matrix [math]\mathbf{C}[/math] which is the sum of two other matrices representing the real [math]\mathbf{R}[/math] and the imaginary [math]\mathbf{I}[/math] parts (note that bold, upper-case characters represent matrices):
Which can also be expressed in the more familiar form of the complex number:
where [math]\mathbf{\hat{R}}{\equiv}1[/math] and [math]\mathbf{\hat{I}}{\equiv}i[/math].
The matrix equivalent of 1 is the 2 x 2 identity matrix:
And as was mentioned in the section titled Powers of i the imaginary component [math]i[/math] can be treated as a 90° counter-clockwise rotation in the complex plane which can also be represented by a rotation matrix:
Now we can express the complex number in matrix form:
So what you see in the section titled Rotors is the matrix form of a complex number and the [math]a[/math] and [math]b[/math] are the real and imaginary parts of a complex number and rotating a complex number (represented in matrix form) by the 2×2 counter-clockwise rotation matrix produces another complex number (represented in matrix form).
It is also interesting to note that if we express the equation [math]i^2=-1[/math] in matrix form we get:
which verifies that the square of the imaginary number is -1.
I hope this helps.
I think there’s a little typo in http://3dgep.com/?p=1815#Quaternion_Dot_Product
It should be q1q2, not q12.
Carlo,
Thanks for pointing this out. It should actually be:
I recently switched LaTeX engines. The new one seems to be a bit more picky about separating parts of the equation for correct rendering.
Thank you ! THANK YOU ! this is an awesome website you made, and while the subjects are technical, they remain accessible… thanks again !
Thank you sooo much for this explanation! I searched for good ones in the web for nearly a month and this is far the best and most detailed I read. Now I can implement Quaternion rotation without shaming me for not knowing the stuff I am using…
A very very very good explanation on quaternions. This is awesome. Well done 🙂
Many thanks for this extraordinary introduction into quaternions.
I really appreciate this work!
Thank you.
You don’t know how many sites I went to trying to find good explanations of Quaternions before ending up here. Keep up the magnificent work. =3
HANDS DOWN. The best tutorial of quaternion ever. It’s step-by-step, ordered from easy to hard, with simple figures.
Hello, I am a little confused about whether I, j and k are all equal to the square root of -1 or whether they are Cartesian unit vectors. To my mind I cannot see how in one step you can multiply a Cartesian unit vector and get -1 and still say their cross product is another unit vector. Are you defining I, j, and k as imaginary numbers or as unit vectors? I don’t think mathematically you define the I, j and k to be both imaginary numbers AND unit vectors as surely numbers and vectors are completely different mathematical objects?
I would really appreciate a reply to this question as I otherwise very impressed with the presentation that you have laid out above.
I’m sorry about the confusion. When the imaginary numbers (\(i\), \(j\), and \(k\)) are shown using emphasis then they represent an imaginary number (along a particular imaginary axis). When they are shown in bold (\(\mathbf{i}\), \(\mathbf{j}\), and \(\mathbf{k}\)) then they represent the basis vectors in the cartesian plane (which have properties similar to the imaginary numbers). This is similar to how the real numbers (\(x\), \(y\), and \(z\)) are used to represent the components of a 3D vector while the basis vectors are represented as \(\mathbf{x}\), \(\mathbf{y}\), and \(\mathbf{z}\) using a boldface font.
I hope this answers you question.
Why would anyone use the that formula for SLERP which divides by sin(theta)?!
((1 – t) q_1 + t q_2)/sqrt(1 + 2 (q1*q2 – 1) (1 – t) t) also yields spherical interpolation, and with this, division by 0 happens only when q1 = -q2 where spherical interpolation isn’t well-defined, because there is no unique path from the north pole to the south pole which makes more sense than any other.
Jens,
Can you provide a reference to your SLERP equation that shows a proof of the equation you are providing?
The SLERP method that uses \(\sin\theta\) provides a method of spherical interpolation that maintains a constant angular velocity while rotating between \(q_1\) and \(q_2\). Note that it does not provide a method to maintain linear velocity over the curve. If the quaternions are not normalized, you may notice some “ease-in” and “ease-out” effects. But this is not a problem if the quaternions are normalized.
Perhaps your formula can better achieve constant linear velocity while allowing for non-normalized quaternions?
As of this time and user, you latex isn’t working.
David,
Thank you for pointing this out. I recently moved 3dgep.com to a new server and the latex and dvipng binaries were not installed on the new server. I have since resolved the issue and confirmed that the equations are showing up now.
I am looking into using a different plugin (MathJax) to have the client browser generate the equations instead of relying on a server side script to generate gifs for all of the equations.
Please let me know if you find any other cases where equations are not being rendered correctly.
Found this great quote for visualization of quaternions. ”Imagine you have a small lump of clay and a load of tooth pics. Slide a tooth pick through the clay on each of it’s individual axis, X, Y and Z. Rotate the tooth picks, notice how the clay is being rotated on one of it’s axis at a time. This is how normal Euler axis work, and how most people understand rotation. Now, grab another tooth pick and jam it into the clay at any angle you want! Rotate the new tooth pick on it’s own axis, notice it isn’t constrained to the x, y or z axis but is rotating on it’s own ‘new’ and unique axis. This ^ is a quaternion, whenever you are reading up on them from now on, think of this example and hopefully it should make a little more sense.”
Your article probe deep into quaternion, which remains a mystery for a long time for me. But I have to questions.
1) In the second example of the “rotations” part. It seems that the vector p = [2, 0, 0] revolves 60 degrees instead of 90 since the angle between p and v is 60. Therefore, the deduction of the “rotor” in quaternion form seems to be incorrect.
2) I try to get a formula of rotors in quaternion form and I get one. But somehow I could not get the correct result with p = [2, 0, 0] and v = [sqrt(2) / 2, 0, sqrt(2) / 2]. I calculated for more than 10 times, the formula seems to be correct.
(Here I ignore my uncertainties I talked about in 1))
The formula I get is:
q*p*inverse(p) = p + sin(theta) * cross(v, p) – sin(theta / 2) * sin(theta / 2) * cross(cross(v, p), v)
And it would be great if we visitors could insert mathematics formula directly into the comment area using LaTex. Good for other visitors since using plain text to represent formulas are seriously ugly!
You should be able to add LaTeX formulas using the [math] shortcode. For example [math]y=x^2[/math] should produce [math]y=x^2[/math].
For example:
\[ \displaystyle\pi(x) = \sum_{n = 1}^\infty \frac{\mu(n)}{n} J(\sqrt[n]{x}) \]
Should produce:
\[ \displaystyle\pi(x) = \sum_{n = 1}^\infty \frac{\mu(n)}{n} J(\sqrt[n]{x}) \]
Hi,
while your formulae are correct, an explanation is missing
why in qp=(q0p0-q1p1-q2p2-q3p3,…. 3 components are subtracted
and in dot(q,p)=q0p0+q1p1+q2p2+q3p3.
It is so in complex and/or quaternion dot product one argument is
taken conjugate before multiplying so eg: q conjg(p) = (dot(q,p),….)
Pingback: Rotations – DubiouSoft
DubiouSoft,
I’ve read your post and I just want thank you for your very kind words. I’m sincerely flattered.
Really nitpicking here, but there should also be no backslash at the end of the equation:
is very small then <img src="https://www.3dgep.com/cgi-bin/mathtex.cgi?\sin\theta\"
Should probably read:
is very small then <img src="https://www.3dgep.com/cgi-bin/mathtex.cgi?\sin\theta"
Cheers
Sylvia,
Thanks for pointing this out. I didn’t really notice anything wrong with the equation, but I fixed it anyways according to your comments.
Oh, it seems my first comment was not posted, so here goes.
Really amazing and detailed write up. Love it. Just a small correction of a missing space $\Delta q$, that lets Latex not displaying this equation properly
Cheers
Another great catch! I’ve fixed the equation now. Thanks for your keen observations Sylvia.
Also, comments don’t appear until they have been approved.
This is the best explanation of quaternions I’ve ever seen! I’ve looked at many others. I finally understand that vector rotation with quaternions is just a couple of multiplications, instead of applying a whole matrix to a vector. Thanks Jeremiah!
Thank you for the best explanation of quaternions! But I have one question about it: in the “rotation” part, you said the “the vector has been rotated 90° rather than 45°”. As the diagram showing, the \(\mathbf{p}\) vector is \([2,0,0]\) and the \(p^{\prime}\) vector is \([1,\sqrt{2},1]\), so the angle between them is \(\cos\theta=\cfrac{p\cdot p^{\prime}}{|p||p^{\prime}|}=\cfrac{1}{2}\), that is θ=60 instead of 90. Am I right? Any suggestion are appreciated.
Babala,
You are right that the dot product between the two pure quaternions (\(p\) and \(p^{\prime}\) is 60° but in the example, \(p\) is rotated 90° about the circle that is formed by the quaternion \(q\). The dot product of the quaternions is similar to that of vectors, it measures the angle formed between the two quaternions. In this case, its the linear angle between the two vectors \(\mathbf{p}\) and \(\mathbf{p^{\prime}}\) but the the rotation is measured about the circle that is swept out by the rotation. Perhaps an image will help illustrate this.
The image visualizes the rotation as observed from looking down the \(k\) (\(z\)) axis. In this image we see that the angle between \(\mathbf{p}\) and \(\mathbf{p^{\prime}}\) is 60° but the semicircle swept out by the rotation is 90°. The next image shows it from a different angle.
This image shows the exact same rotation but now we are looking directly at the axis of rotation. Now it can easily be observed that \(p\) has been rotated exactly 90° about the quaternion axis.
So the quaternion dot product does not measure the amount of rotation that is applied, but just the angle between the vector parts of the two quaternions.
Keep in mind that if the point being rotated is very close to the axis of rotation, the circle swept by the rotation will be very small. In this case, the dot product between the original point and the rotated point may be very small (almost 0), but the amount the point was rotated could be ±180°
I hope this answers your question.
For example,
Einstein’s theory of special relativity is \(E=mc^2\).
And the gaussian integral is:
\[ \int_{-\infty}^\infty e^{-x^2}dx = \sqrt{\pi} \]
Should produce:
Einstein’s theory of special relativity is \(E=mc^2\).
And the gaussian integral is:
\[ \int_{-\infty}^\infty e^{-x^2}dx = \sqrt{\pi} \]
Hello, Just to let you know that I like your tutorial and the clarity it brings to the subject.
I am just completing another book Imaginary Mathematics for Computer Science.
Best wishes.
Thanks John for your wonderful book on Quaternions that has inspired this article. It has help a lot of people (including myself) to better understand how quaternions can be used in graphics applications!
I will definitely be looking forward to your next book!
Thanks for your enlightling article, Jeremiah. I benefited a lot from it. But “Negating the scalar and the vector part of the quaternion does not change the orientation that it represents” has confused me at first. Finally, I realized that what you mean might be that a quaternion or its “negative quaternion” could leads to the same rotation result despite the difference of rotation direction. However, I think it is still not appropriate to say that a quaternion and its “negative quaternion” represent the same orientation, cause they actually do have a angular difference of 180°.
I got a typo, it is “enlightening”
This is an excellent article. Thank you very much! It helped me understand some of 3D transformations I’ve been struggling with! A very good way to understand quaternions in 3D graphics when applied to simple rotations is as “a vector representing the axis of rotation plus the angle of rotation”. Most of math libraries with quaternions allow you to create a quaternion like that which is very easy to grasp.
I love the way you illustrate expressions as clear concepts. Excellent article. I will definitely stick on this website for a long while.
Hello, i would like to know why it was imposible for Hamilton to multiply with his 3 term quaternions?
Great article for those brave enough to trudge thru the math. I finally got up the courage and glad that i did. Thanks
Small typo: I’m guessing ‘Were, according to Hamilton’s famous expression:’
should be ‘Where, according to Hamilton’s famous expression:
Mike,
Thanks for pointing this out! I’ve corrected the text 🙂
Hey! First of all thanks for very nice article it is really helpful.
I would like to point out an ambiguity in notations. In rotations section, \(q^{-1}\) is actually the conjugate if I am not mistaken, not the inverse. Thus, it creates an ambiguity with the definitions made before and other articles about the topic. I would humbly suggest changing the rotation formulation to \(qpq^*\). Again ofc. if I am not mistaken:)
Best
Barış
Baris,
I checked several sources for quaternion notation and this is what I found:
So from these references, I think it is safe to say that there is no ambiguity using \(q^*\) to denote the quaternion conjugate. Perhaps your confusion comes from the fact that the unit norm quaternion conjugate is the inverse. This is equivalent to the fact that the transpose of an orthonormalized matrix is its inverse.
Thanks for the detailed reply!
Yeah you are on spot about my source of confusion:) We are on the same page about q^* by the way. It was a bit confusing at rotation formula only, where it is qpq^-1 but since your explanation everything is clear now thanks!
Best.
Thanks for this very nice tutorial.
I have enjoyed all your articles and this is no exception. I would like to add with this link below in response to “Don’t try to actually understand this term as there is no logical reason why it exists. We just have to accept that i is just something that squares to −1.”
I feel like it gives a good history behind complex numbers and because of it, I always replace imaginative with lateral when I read i.
https://www.youtube.com/watch?v=T647CGsuOVU
Best regards
Ryan
Ryan,
Thanks for the link!
thinks for you job; it give me deep understanding of Quaternion and Matric.
Dear Jeremiah Hello.
I’m not doing graphics but firmware for embedded ARM Cortex-Mn designs and C++/CUDA programming for large datasets processing. Looking for a solution to a problem irrelevant to my work but very relevant to some research that I’m doing I located your site and as a Physicist I was intrigued by this quaternion page and the Understanding Quaternions example that I downloaded and run. I think that this approach may answer to my query, but I don’t yet know how. My query goes as following:
We are given a 2D spiral of step let’s say a, that lays on the X-Z plane with its center found at (0,0,0). What would be the solid structure emerging by a revolution of that spiral about the X or the Z axis from 0 to π ? I would greatly appreciate if a quaternions based example, like your example above, could be produced for seeing this in action.
Thank you very much.
John
John,
Hmm.. This doesn’t seem like something I can just whip up in a comment reply. Please consider joining the Discord server: https://discord.gg/gsxxaxc
There are community members that might be willing to help you with your research.
Thanks for a very good and comprehensive article.
But i have a question about the graphic of “Visualizing the Properties of ij, jk, ki”.
So, if it is a cross product, should not the area between multiplied axis’ shaded?
Otherwise, if we think it like rotation that for x * y, y rotates x axis onto z so the area of z-x should be shaded.
I suppose it is not entirely accurate to visualize this relationship as a “rotation”. It’s more like a mnemonic to try to remember the relationship. If it helps you to think of it the other way around, then I suppose that is also valid.
Another way I like to visualize it, is to place \(i\), \(j\), and \(k\) in the columns of a matrix:
\[
\left[
\begin{array}{ccc|ccc}
i & j & k & i & j & k \\
i & j & k & i & j & k \\
i & j & k & i & j & k \\
\end{array}
\right]
\]
Then, if you take the (forward) diagonal entries of the matrix , you get the same order. If you take the backward diagonal, you get the inverse:
\[
\begin{array}{ccc}ij=k & jk=i & ki=j \\ ji=-k & kj=-i & ik=-j\end{array}
\]
Isn’t my edit what the author wanted to convey? If not can somebody explain this to me? If you multiply the matrices in my version you get a’ + b’i formula from above.
Thanks,
Tyler
For clarity, Tyler wants to know if:
\(\begin{bmatrix} a^{\prime} & -b^{\prime} \\ b^{\prime} & a^{\prime} \end{bmatrix}=\begin{bmatrix} \cos\theta & -\sin\theta \\ \sin\theta & \cos\theta \end{bmatrix}\begin{bmatrix}a & -b \\b & a \end{bmatrix}\)
should be written like:
\(\begin{bmatrix} a^{\prime} \\ b^{\prime} \end{bmatrix}=\begin{bmatrix} \cos\theta & -\sin\theta \\ \sin\theta & \cos\theta \end{bmatrix}\begin{bmatrix}a \\b \end{bmatrix}\)
(In the section about Rotors)
I think this is valid if we are only interested in the result of the real (\(a\)) and the imaginary (\(b\)) parts of the equation.
Its derivation is simply wrong, although the rotation matrix is correct.
p’ = qp is simply wrong.
p’=qpq* is the correct formula
I think you are referring to quaternion rotation?
I suppose if the quaternion was normalized, you could use the conjugate, but the general formula is:
\[ p’=qpq^{-1} \]
If you read a little bit further, we come to this conclusion:
I hope this clears it up?
Hi Jeremiah,
Great article and good explanation on the Quaternions, thanks!
Also thanks for the demo “Understanding Quaternions”. I have got the personal version of Unity (ver. 2019.4.1711). Just wondering if you could provide a quick step-by-step guide on how to load your demo? I am new to Unity so a little help would be very much appreciated. Thank you very much and happy new year!
Regards,
Eric
Eric,
There should be an executable file in the Build folder. Running that will show a cube with some arrows pointing out of it. Use the slider to adjust the quaternion rotation (0 … 360 degrees). Press the X, Y, or Z buttons to align the quaternion to one of those axis, or press the center of the cube and drag out to create a rotation quaternion. Slide the slider to see how the cube rotates depending on the quaternion axis.
I hope this helps!
This is a really wonderful write-up! I’ve been scouring the internet to find some resource that would just explain quaternions in an intuitive, ground-up way, and thank god I stumbled upon this because it might be the only post that actually accomplishes this 🙂
Thank you, It is great article. I have a real programming problem. I have two quaternion values coming from two different sensor. I need to calculate real smallest angle (and also angle in one direction) between two sensors.
Really a wonderful article! Especially the Quaternion Interpolation, it is very helpful for the robot orientation interpolation! Thank you very much!
It is very well presented. But some how two topics are left dangling:
1. quaternions with half angles : q P q* will do the trick. can show it will result . And the vector part can be shown as a correct rotation.
details: use unit vector v as i , v P plane as i j plane,
vector v cross multiply vector P as k,
and tilda = angle between v and P
then: P= cos(tilda) i + sin(tilda) j
q Pq* = cos(tilda)i+ sin(tilda)cos(theta)j+ sin(tilda)sin(theta)k
where theta is angle of rotation
then magnitude of one is reserved and space rotaton recognized.
.
the second comment is the beautiful plot of vector Vt in the spherical interpolation. It is a pity to draw V1 and V2 as orthogonal.
We can put V1 and V2 as two unit vectors on the unit circle, ( with V1 dot V2 =cos (theta) = cos(alpha+ beta)). Then it can be shown Vt = sin(beta)/sin(theta) V1+ sin(alpha)/sin(theta) V2 will also be a unit vector on the unit circle. In fact, Vt component in V1 direction is cos (alpha) and its V1 vertical component is sin (alpha). Hence, its magnitude is one, and lies on the unit circle. It will be interesting if we can show it in a picture here.
I am commenting because your work inspires me. :).
So, in reality, Hamilton “discovered” the cross product, well before Gibbs is credited for it in 1881. Not only did he discover it but straight applied to 3D.
BTW this website is the cleanest explanation i’ve come across. Seriously.
Dear Jeremiah,
Hello.
I am a novice programmer and just learning about quaternions and was hoping you could give me some suggestions on how to handle quaternions offsets in 3D that dynamically change. For example, I am working on a small demo in which I’ve positioned a camera behind a 3D pirate model who is standing on a pirate ship. My demo has toggle buttons which attach and detach from the pirate model. When the attach button is pressed the camera becomes the parent of the pirate and moves the pirate around the pirate ship in 3D. When the detach button is pressed the camera is no longer the pirate’s parent and the pirate remains anchored to his position on the pirate ship while the user is free to explore around the ship using just the camera. Then when the user presses the attach button again, the camera becomes the parent again of pirate model in the proper orientation of wherever the user last left the pirate on the deck.
The problem I am having is that the 3D pirate model orientation is face down when it gets loaded into the demo project. Thus, in the setup, I first orient the pirate face up (vec3 (-90,0,0) in Euler angles)). Yet the camera parent starts off being correctly orientated (i.e. 90 degrees offset from the pirate model I want it to follow). Thus, when setting the camera’s quat orientation to match the pirate, I start off by offsetting it by 90 degrees (e.g):
cameraQuatRotation = quatEquivalentOfEuler(90,0,0) * PirateQuatRotation
That works initially but likely because the pirate starts off being orientated on the x-axis in world space. However, the offset equation fails when I start to move the pirate off his original axis (e.g. so the pirate’s feet are now orientated along the z-axis in world space. It seems I somehow need to dynamically change the offset of my above equation from:
QuatEquivalentOfEuler(90,0,0)
To a new dynamically generated one:
QuatEquivalentOfEuler(vec3(90,0,0) converted to that offset vector equivalent after the pirate has been rotated).
Any suggestions?
I appreciate any help you could provide and am happy to clarify the question if needed.
Thank you.
This is an elaborate question and not something I can answer in a comment thread. Plase consider joining our Discord server: https://discord.gg/gsxxaxc
what tool was used to draw the diagrams?
I use Adobe Illustrator for all of the diagrams used on this website.
Hi Jeremiah,
I don’t really understand the first image of quaternions (title “Visualizing the Properties of 𝐢𝐣, 𝐣𝐤, 𝐤𝐢”). It is unclear to me what the quarter circle means, ie. the colored gradient – does it imply the measurement of the circle arc (arc of a pi/2 angle) or the area inside the quarter circle? Or perhaps something else.
E.g. the formula 𝐢𝐣=𝐤 is shown with a circle arc from the y-axis to the z-axis – why isn’t this arc connecting the x- and z axes? (Because we are showing 𝐢𝐣, not 𝐣𝐤).
Unless I’m the only one getting confused by this diagram, perhaps you might add some descriptive comment?
Otherwise I’m enjoying reading this a lot, very nice article!
Hi, thanks for this website, it makes me understand quaternion more.
But I still have some questions about how to measure the difference between two quaternions. If we use the dot product we can get the cos(\theta) but we still don’t know the angles, and it can be \theta or \pi + \theta. I am new to this field, so please point out any mistake I took.
Thanks for helping!
Hi, thank you so much for this clear guide. I am writing.a report for school on why quaternions are such a good option for computer graphics, and your article has been incredibly helpful. Do you happen to have a mathematical proof for that post-multiplying qp by q’s inverse restores the norm of any given rotated quaternion?