C++ Templates

In this post, I will introduce you to C++ template programming. Some of the topics I will cover are function templates, class templates, variable templates, variadic templates, type traits, SFINAE, and C++ 20 concepts.

Contents

1 Introduction
2 Terminology
- 2.1 Expressions and Value Categories
- 2.2 Template Arguments versus Template Parameters
3 Basics
4 Template Type Deduction
5 decltype Specifier
6 std::declval()
7 Type Traits
8 SFINAE
9 Concepts
10 Conclusion
11 Bibliography

Introduction

C++ Template Programming has been around for a long time and there are plenty of books and articles on the internet that describe C++ template programming. Although the information is in abundance, there doesn’t seem to be a comprehensive source for learning how to apply template programming and demystify some of the more complex features of C++ template programming such as using and writing type traits, template meta programming, and Substitution Failure Is Not An Error (SFINAE) which are a few of the topics that I would like to cover in this article.

Terminology

Before delving into the details of C++ template programming, it is important to establish some common terminology when describing template programming.

Value categories are a way to categorize how a value can be used. There are five value categories (lvalue, prvalue, xvalue, glvalue, and rvalue). You may already be familiar with lvalue, and rvalue, but might not have encountered prvalue, xvalue, or glvalue yet.

Understanding the difference between template parameters and template arguments is also important when talking about template programming. In short, template parameters are used to declare the template and template arguments are used to define the template. Template parameters can be either typed, or non typed.

Let’s first look at value categories.

Expressions and Value Categories

All C++ programmers work with value categories but may not be able to describe which category a value belongs.

Value categories are often defined in terms of the result of an expression. An example of an expression is assignment, increment and decrement, arithmetic, logical, function calls, etc. An expression consists of one or more operands and one operator (or two operators in the case of the ternary operator). Expressions are usually terminated with a semicolon (;) but can also be nested inside other expressions or used inside conditional constructs (like if, while, and for loops).

A C++ Expression is a sequence of operators and operands that produce a result.

Expressions are categorized according to the following taxonomy:

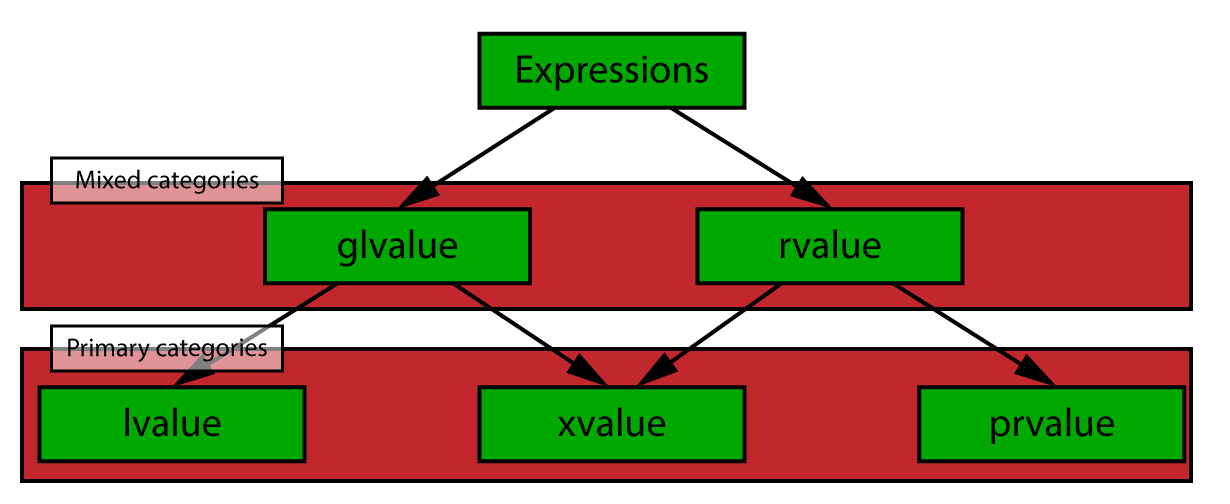
Expressions are categorized according to the following taxonomy.^[6]

According to Stroustrup^[2], value categories can be identified by two independent properties:

“has identity” (i): A value is identified by a name. Pointers and references also represent identities.
“can be moved from” (m): A value can be moved. Expressions that use move semantics like the move constructor and the move assignment operator are examples of move expressions.

When a value category has the identity property, it can be denoted with a lower-case i. When a value type does not have the identity property, it will be denoted with an upper-case I.
Similarly for the move property: if the value category can be moved, it will be denoted with a lower-case m, otherwise it will be denoted with an upper-case M.

There are five value categories (three primary, and two mixed categories) that are discussed in this section:

Primary categories

lvalue
prvalue
xvalue

Mixed categories

glvalue
rvalue

lvalue, prvalue, and xvalue are primary value categories because they are mutually exclusive. glvalue and rvalue categories are mixed categories because they are a generalization of the primary value categories.

lvalue

An lvalue is a value that is named by an identifier (i) but cannot be moved (M). An lvalue is something that has a location in memory. For this reason, lvalues are sometimes referred to as locator values.

The following code snippet shows some examples of lvalues.

int i = 3;                       // i is an lvalue.
std::string s = "Hello, world!"; // s is an lvalue.
int* p = nullptr;                // p is an lvalue.
int& r = *p;                     // r is an lvalue.

int i = 3; // i is an lvalue.

std::string s = "Hello, world!"; // s is an lvalue.

int* p = nullptr; // p is an lvalue.

int& r = *p; // r is an lvalue.

It might be tempting to think of lvalues as something that only appears on the left-hand side of an assignment operator, but this is not a good way to think of them. For example, a const value is an lvalue, but it cannot be assigned to after initialization.

const int i = 3; // i is an lvalue.
i = 4;           // error: assignment of read-only variable 'i'

1 2	const int i = 3; // i is an lvalue. i = 4; // error: assignment of read-only variable 'i'

Of course, lvalues can also appear on the right side of the assignment operator.

const int i = 3; // i is an lvalue.
int j = i;       // i is an lvalue on the right side of the assignment operator.

1 2	const int i = 3; // i is an lvalue. int j = i; // i is an lvalue on the right side of the assignment operator.

However, calling i an lvalue in this context (when it appears on the right side of the assignment operator) is not entirely correct. In this case, i is implicitly cast to an rvalue (the contents of i) which is what gets assigned to j^[4].

An easy way to remember if something is an lvalue is to ask the question “is it possible to take the address of this value?”. If the answer is yes, then the value is an lvalue.

prvalue

A prvalue is a pure rvalue. Pure rvalues do not have an identifier (I) but can be moved (m). Literal values are examples of prvalues.

int i = 3;                       // 3 is a prvalue.
std::string s = "Hello, world!"; // "Hello, world!" is a prvalue.
int* p = nullptr;                // nullptr is a prvalue.
bool b = true;                   // true is a prvalue.

int i = 3; // 3 is a prvalue.

std::string s = "Hello, world!"; // "Hello, world!" is a prvalue.

int* p = nullptr; // nullptr is a prvalue.

bool b = true; // true is a prvalue.

It is possible to assign a prvalue to an lvalue (as demonstrated in the previous code example) but it is not possible to assign an lvalue to a prvalue.

int i = 3; // prvalue 3 is assigned to lvalue i.
int j = 4; // prvalue 4 is assigned to lvalue j.
3 = i + j; // error: lvalue required as left operand of assignment

int i = 3; // prvalue 3 is assigned to lvalue i.

int j = 4; // prvalue 4 is assigned to lvalue j.

3 = i + j; // error: lvalue required as left operand of assignment

It is also an error to try to get the address of a prvalue.

bool* b = &true;      // error: lvalue required as unary '&' operand
int* i = &3;          // error: lvalue required as unary '&' operand
int* j = &( 3 + 4 );  // error: lvalue required as unary '&' operand

bool* b = &true; // error: lvalue required as unary '&' operand

int* i = &3; // error: lvalue required as unary '&' operand

int* j = &( 3 + 4 ); // error: lvalue required as unary '&' operand

The result of an expression using built-in operators are also prvalues.

(1 + 3);         // prvalue
(true || false); // prvalue
(true && false); // prvalue

(1 + 3); // prvalue

(true || false); // prvalue

(true && false); // prvalue

It is possible to override the built-in operators to return non-prvalues, but that is not important in order to describe value categories.

One special thing to note is that prvalues can be candidates for move operations. The following example is valid:

int MoveMe(int&& i) // MoveMe takes an rvalue reference.
{
    int j = i;
    return j;
}

int main()
{
    int i = 0;
    i = MoveMe(3); // prvalue (3) is used where an rvalue reference is expected.
    return 0;
}

int MoveMe(int&& i) // MoveMe takes an rvalue reference.

{

int j = i;

return j;

}

int main()

{

int i = 0;

i = MoveMe(3); // prvalue (3) is used where an rvalue reference is expected.

return 0;

}

This code compiles fine since the prvalue (3) is moved into the i parameter in the MoveMe function.

xvalue

An xvalue are values that are named using an identifier (i) and are movable (m). Any function that returns an rvalue reference (such as std::move) is an xvalue expression. xvalues are the result of casting an lvalue to an rvalue reference as shown in the following example:

int i = 0;              // i is an lvalue.
int&& j = std::move(i); // The result of std::move is an xvalue.

1 2	int i = 0; // i is an lvalue. int&& j = std::move(i); // The result of std::move is an xvalue.

The result of std::move is an xvalue and can be assigned to an rvalue reference.

The xvalue is referred to as an “expiring value” since it is used to refer to an object that is expiring since its resources are likely only going to be moved to another object soon^[5].

The xvalue value category is somewhat esoteric and likely only important for compiler writers and people working on the C++ standard documentation. For this article, it’s only important to know of its existence.

glvalue

A glvalue is a “generalized lvalue”^[2]. glvalues can be either an lvalue or an xvalue. You can think of it as a movable (m) lvalue. glvalues can also be named by an identifier (i). Some examples of glvalues are:

int i;       // i is a glvalue (lvalue)
int* p = &i; // p is a glvalue (lvalue)
int& f();    // the result of f() is a glvalue (lvalue)
int&& g();   // the result of g() is an glvalue (xvalue)

int i; // i is a glvalue (lvalue)

int* p = &i; // p is a glvalue (lvalue)

int& f(); // the result of f() is a glvalue (lvalue)

int&& g(); // the result of g() is an glvalue (xvalue)

A glvalue is anything that is not a prvalue.

rvalue

An rvalue is a generalization of prvalues and xvalues. An rvalue is not named with an identifier (I) but can be moved (m). To avoid ambiguity with prvalues, rvalues are only denoted with the lower-case (m) to indicate the value “can be moved from”.

int i = 3;                       // 3 is an rvalue (prvalue).
std::string s = "Hello, world!"  // "Hello, world!" is an rvalue (prvalue)
int&& g();                       // The result of g() is an rvalue (xvalue)

int i = 3; // 3 is an rvalue (prvalue).

std::string s = "Hello, world!" // "Hello, world!" is an rvalue (prvalue)

int&& g(); // The result of g() is an rvalue (xvalue)

An rvalue is anything that is not an lvalue.

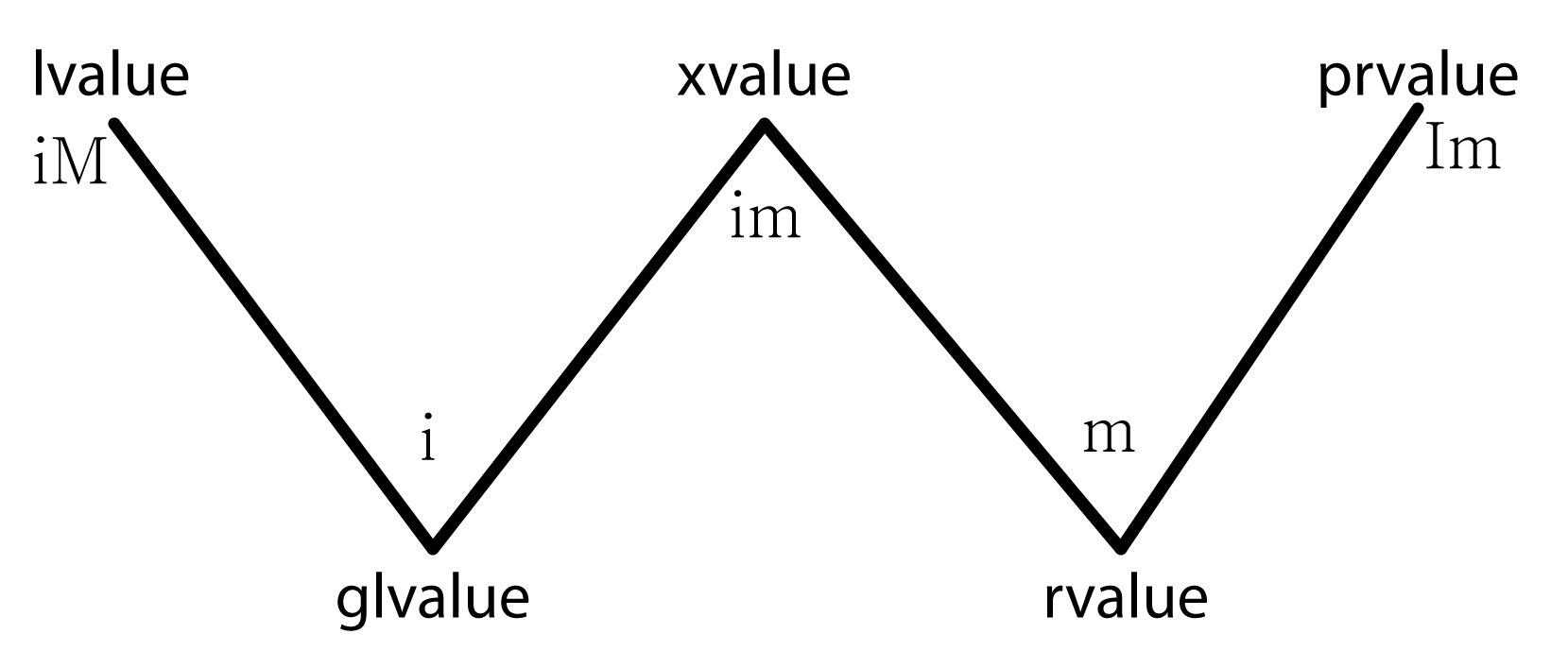
This images shows the various value categories and their corresponding properties as depicted by Bjarne Stroustrup^[2].

Template Arguments versus Template Parameters

Suppose we have the following template class:

template<typename T, size_t N>
class Array
{
public:
    Array()
        : m_Data{}
    {}

    size_t size() const
    {
        return N;
    }

    T& operator[](size_t i)
    {
        assert(i < N);

        return m_Data[i];
    }

    const T& operator[](size_t i) const
    {
        assert(i < N);

        return m_Data[i];
    }

private:
    T m_Data[N];
};

template<typename T, size_t N>

class Array

{

public:

Array()

: m_Data{}

{}

size_t size() const

{

return N;

}

T& operator[](size_t i)

{

assert(i < N);

return m_Data[i];

}

const T& operator[](size_t i) const

{

assert(i < N);

return m_Data[i];

}

private:

T m_Data[N];

};

And we also have the following instantiation of the template class:

Array<float, 3> Position;
Array<float, 3> Normal;
Array<float, 2> TexCoord;

Array<float, 3> Position;

Array<float, 3> Normal;

Array<float, 2> TexCoord;

In this example, the template parameters are T and N and the type template argument is float and the non-type template arguments are 3, and 2. You can say that “parameters are initialized by arguments“.

Unlike function arguments, value of non-type template arguments must be determined at compile-time and the definition of a template with its arguments is called the template-id.

Each parameter in a template parameter list can be one of following types:

A type template parameter
A non-type template parameter
A template template parameter

The Array class template demonstrates the use of both type (T), and non-type (N) template parameters. In the next section, all three parameter types are explored.

Type Template Parameter

The most common template parameter is a type template parameter. A type template parameter starts with either typename or class and (optionally) followed by the parameter name. The name of the parameter is used as an alias of the type within the template and has the same naming rules as an identifier used in a typedef or a type alias.

A type template parameter may also define a default argument. If a type template parameter defines a default value, it must appear at the end of the parameter list.

A type template parameter can also be a parameter pack. A parameter pack starts with typename... (or class...) and is used to list an unbounded number of template parameters. Since parameter packs apply to all template parameter categories, parameter packs are discussed in the section about template parameter packs.

The following example demonstrates the use of type template parameters.

// typename introduces a type template parameter.
template<typename T> class Array { ... }; 

// class also introduces a type template parameter.
template<class T> struct MyStruct { ... }; 

// A type template parameter with a default argument.
template<typename T = void> struct RType { ... };

// The parameter name is optional.
template<typename> struct Tag { ... };

// typename introduces a type template parameter.

template<typename T> class Array { ... };

// class also introduces a type template parameter.

template<class T> struct MyStruct { ... };

// A type template parameter with a default argument.

template<typename T = void> struct RType { ... };

// The parameter name is optional.

template<typename> struct Tag { ... };

Non-type Template Parameter

Non-type template parameters can be used to specify a value rather than a type in the template parameter list.

Non-type template parameters can be:

An integral type (bool, char, int, size_t, and unsigned variants of those types)
An enumeration type
An lvalue reference type (a references to an existing object or function)
A pointer type (a pointer to an existing object or function)
A pointer to a member type (a pointer to a member object or a member function of a class)
std::nullptr_t

C++20 also adds floating-point types and literal class types (with some limitations explained here) to the list of allowed non-type template parameters.

Similar to type template parameters, the name of the template parameter is optional and non-type template parameters may also define default values.

The following shows examples of non-type template parameters:

// Integral non-type template parameter.
template<int C> struct Integral {};

// Also an Integral non-type template parameter.
template<bool B> struct Boolean {};

// Enum non-type template parameter
template<MyEnum E> struct Enumeration {};

// lvalue reference can also be used as a non-type template parameter.
template<const int& C> struct NumRef {};

// lvalue reference to an object is also allowed.
template<const std::string& S> struct StrRef {};

// Pointer to function
template<void(*Func)()> struct Functor {};

// Pointer to member object or member function.
template<typename T, void(T::*Func)()> struct MemberFunc {};

// std::nullptr_t is also allowed as a non-type template parameter.
template<std::nullptr_t = nullptr> struct NullPointer {};

// Floating-point types are allowed in C++20
template<double N> struct FloatingPoint {};

// Literal class types are allowed in C++20.
template<MyClass C> struct Class {};

// Integral non-type template parameter.

template<int C> struct Integral {};

// Also an Integral non-type template parameter.

template<bool B> struct Boolean {};

// Enum non-type template parameter

template<MyEnum E> struct Enumeration {};

// lvalue reference can also be used as a non-type template parameter.

template<const int& C> struct NumRef {};

// lvalue reference to an object is also allowed.

template<const std::string& S> struct StrRef {};

// Pointer to function

template<void(*Func)()> struct Functor {};

// Pointer to member object or member function.

template<typename T, void(T::*Func)()> struct MemberFunc {};

// std::nullptr_t is also allowed as a non-type template parameter.

template<std::nullptr_t = nullptr> struct NullPointer {};

// Floating-point types are allowed in C++20

template<double N> struct FloatingPoint {};

// Literal class types are allowed in C++20.

template<MyClass C> struct Class {};

Non-type template parameters must be constant values that are evaluated at compile-time.

Template Template Parameter

Templates can also be used as template parameters:

// C is a template class that takes a single type template parameter.
template<template<typename T> class C> struct TemplateClass {};

// C is a template class that takes a type and non-type template parameter.
template<template<typename T, size_t N> class C> struct ArrayClass {};

// keyword typename is allowed in C++17.
template<template<typename T> typename C> struct TemplateTemplateClass {};

// C is a template class that takes a single type template parameter.

template<template<typename T> class C> struct TemplateClass {};

// C is a template class that takes a type and non-type template parameter.

template<template<typename T, size_t N> class C> struct ArrayClass {};

// keyword typename is allowed in C++17.

template<template<typename T> typename C> struct TemplateTemplateClass {};

Note that until C++17, unlike type template parameters, template template parameters can only use the keyword class and not typename.

Template Parameter Pack

A template parameter pack is a placeholder for zero or more template parameters. A template parameter pack can be applied to type, non-type, and template template parameters but the parameter types cannot be mixed in a single parameter pack.

A few examples of template parameter packs:

// Function template with a parmeter pack.
template<typename... Args> void func(Args... args);

// Type template parameter pack.
template<typename... Args> struct TypeList {};

// Non-type template parameter pack.
template<size_t... Ns> struct IntegralList {};

// Template template parameter pack.
template<template<typename T> class... Ts> struct TemplateList {};

// Function template with a parmeter pack.

template<typename... Args> void func(Args... args);

// Type template parameter pack.

template<typename... Args> struct TypeList {};

// Non-type template parameter pack.

template<size_t... Ns> struct IntegralList {};

// Template template parameter pack.

template<template<typename T> class... Ts> struct TemplateList {};

A pack that is followed by an ellipsis expands the pack. A pack is expanded by replacing the pack with a comma-separated list of the template arguments in the pack.

For example, if a function template is defined with a parameter pack:

template<typename... Args>
void func(Args... args)
{
    std::tuple<Args...> values(args...);
}

template<typename... Args>

void func(Args... args)

{

std::tuple<Args...> values(args...);

}

And invoking the function:

func(4, 3.0, 5.0f);

1	func(4, 3.0, 5.0f);

Will result in the following expansion:

void func(int arg1, double arg2, float arg3)
{
    std::tuple<int, double, float> values(arg1, arg2, arg3);
}

void func(int arg1, double arg2, float arg3)

{

std::tuple<int, double, float> values(arg1, arg2, arg3);

}

More examples of using template parameter packs are shown later in the section about variadic templates.

Basics

The following sections introduce the basics of templates. If you are already familiar with templates, then you may want to skip to the next section.

Function Templates

Function templates provide a mechanism to define a function that operates on different types. Function templates look like ordinary functions but start with the template keyword followed by a list of (one or more) template parameters surrounded by angle brackets.

template<typename T>
T max(T a, T b)
{
    return a > b ? a : b;
}

template<typename T>

T max(T a, T b)

{

return a > b ? a : b;

}

The max function accepts a single template parameter T. The max function template defines a family of functions that can take different types. The type is defined when the function is invoked either by explicitly specifying the type or by allowing the compiler to deduce the type:

int m = max<int>(3, 5); // Explicit type.
int n = max(3, 5);      // Implicit type deduction.

1 2	int m = max<int>(3, 5); // Explicit type. int n = max(3, 5); // Implicit type deduction.

On the first line, int is explicitly provided as the template argument. On the second line, the template argument is not specified but the complier automatically deduces it as int because the 3 and the 5 are deduced as int. In both cases, the same function is instantiated.

Implicit template type deduction does not work if you want to mix types as in the following case:

double x = max(3, 5.0);

1	double x = max(3, 5.0);

In this case, the max function template is being instantiated with 3 (int) and 5.0 (double) and the compiler does not know how to implicitly determine the template argument. In this case, the compiler will generate an error. There are a few ways this can be fixed:

Use an explicit template argument
Cast all function arguments to the same type
Multiple template parameters

Explicitly specifying the template arguments will ensure that all of the parameters are cast to the correct type through implicit casting:

double x = max<double>(3, 5.0);

1	double x = max<double>(3, 5.0);

3 is implicitly cast to a double. In this case, the compiler may not even issue a warning since this type of cast does not cause any truncation of the original type. However, if a narrowing conversion occurs, the compiler will very likely generate a warning. To avoid this warning, an explicit cast can be used:

int x = max(3, static_cast<int>(5.0));

1	int x = max(3, static_cast<int>(5.0));

In this example, an explicit cast is used to convert 5.0 from a double to an int. The compiler no longer generates a warning and T is implicitly deduced to int.

The other solution to this problem is to allow a and b to be different types:

template<typename T, typename U>
T max(T a, U b)
{
    return a > b ? a : b;
}

template<typename T, typename U>

T max(T a, U b)

{

return a > b ? a : b;

}

Now a and b can be different types and we can call the function template with mixed types without the compiler issuing any warnings… right? What about the return type? If T is “narrower” than U then the compiler will have to perform a narrowing conversion again and likely issue a warning when this happens. So what should the return type be? Is it possible to let the compiler decide?

Since the compiler will do anything to prevent data loss, it will try to convert all arguments to the largest (widest) type before performing the comparison and the return type will be the widest type. We can use the auto return type deduction, trailing return type, and the decltype specifier to automatically determine the safest type to use for the return value of the function template:

template<typename T, typename U>
auto max(T a, U b) -> decltype(a > b ? a : b)
{
    return a > b ? a : b;
}

template<typename T, typename U>

auto max(T a, U b) -> decltype(a > b ? a : b)

{

return a > b ? a : b;

}

The trailing return type can be omitted in C++14 and higher.

This version of the max function template may still generate a warning about returning a reference to a temporary, but we can use type traits to avoid this. Type traits are discussed later so I won’t complicate this example more than necessary for now.

Using this version of the function template, any type can be used for a and b and the return value is the widest type of a or b. For example:

auto x = max(3.0, 5);

1	auto x = max(3.0, 5);

x is automatically deduced to double because comparing 3.0 (double) and 5 (int) results in a conversion to double and the max function template returns double.

The decltype specifier is explained in more detail later.

There is also a solution to determine the return type using std::common_type but requires knowledge of type traits which is discussed later.

Class Templates

Similar to Function Templates, classes can also be parameterized with one or more template parameters. The most common use case for class templates are containers for other types. If you have used any of the container types in the Standard Template Library (STL) (such as std::vector, std::map, or std::array), then you have already used class templates. In this section, I describe how to create class templates.

Consider the Array class template from the previous section. Here it is again for clarity:

template<typename T, size_t N>
class Array
{
public:
    Array()
        : m_Data{}
    {}

    size_t size() const
    {
        return N;
    }

    T& operator[](size_t i)
    {
        assert(i < N);

        return m_Data[i];
    }

    const T& operator[](size_t i) const
    {
        assert(i < N);

        return m_Data[i];
    }

private:
    T m_Data[N];
};

template<typename T, size_t N>

class Array

{

public:

Array()

: m_Data{}

{}

size_t size() const

{

return N;

}

T& operator[](size_t i)

{

assert(i < N);

return m_Data[i];

}

const T& operator[](size_t i) const

{

assert(i < N);

return m_Data[i];

}

private:

T m_Data[N];

};

A class template that doesn’t specialize any template parameters is called the primary template.

The Array class template demonstrates two kinds of template parameters:

Type template parameters (denoted with typename or class)
Non-type template parameters (denoted with an integral type such as size_t)

The Array class template defines a simple container for a static (fixed-size) array similar to the std::array implementation from the STL.

Inside the Array class template, T can be used wherever a type is expected (such as the declaration of the m_Data member variable or the return value of a member function) and N can be used wherever the number of elements is required (such as in the assert‘s in the index operator member functions).

A class template is instantiated when a variable that uses the class is defined:

Array<float, 3> Position;
Array<float, 2> TexCoord;

1 2	Array<float, 3> Position; Array<float, 2> TexCoord;

Here, Array<float, 3> represents the type of the Position variable and Array<float, 2> is the type of the TexCoord variable. Although both types are instantiated from the same class template, they are in no way related. You cannot use Array<float, 3> where an Array<float, 2> is expected. For example, the following code will not compile:

Array<float, 2> add(const Array<float, 2>& a, const Array<float, 2>& b)
{
    Array<float, 2> c;
    
    c[0] = a[0] + b[0];
    c[1] = a[1] + b[1];

    return c;
}

...

Array<float, 3> Position1;
Array<float, 3> Position2;

auto Position3 = add(Position1, Position2); // Error: Array<float, 3> is not compatible with Array<float, 2>

Array<float, 2> add(const Array<float, 2>& a, const Array<float, 2>& b)

{

Array<float, 2> c;

c[0] = a[0] + b[0];

c[1] = a[1] + b[1];

return c;

}

...

Array<float, 3> Position1;

Array<float, 3> Position2;

auto Position3 = add(Position1, Position2); // Error: Array<float, 3> is not compatible with Array<float, 2>

Although this is a pretty contrived example, it demonstrates that different combinations of template arguments create different (unrelated) types.

Variable Templates

Variable templates were added to the C++ standard with C++14. Variable templates allow you to define a family of variables or static data members of a class using template syntax.

template<typename T>
constexpr T pi = T(3.1415926535897932384626433832795L);

1 2	template<typename T> constexpr T pi = T(3.1415926535897932384626433832795L);

The variable template pi can now be used with varying levels of precision:

std::cout << std::setprecision(30);
std::cout << PI<int> << std::endl;
std::cout << PI<float> << std::endl;
std::cout << PI<double> << std::endl;

std::cout << std::setprecision(30);

std::cout << PI<int> << std::endl;

std::cout << PI<float> << std::endl;

std::cout << PI<double> << std::endl;

Will print:

3
3.1415927410125732421875
3.14159265358979311599796346854

3.1415927410125732421875

3.14159265358979311599796346854

Variable templates can also have both type and non-type template parameters:

template<typename T, T N>
constexpr T integral_constant = N;

1 2	template<typename T, T N> constexpr T integral_constant = N;

T is a type template parameter and N is a non-type template parameter of type T.

It’s important to understand that a variable template does not define a type, but rather a value that is evaluated at compile-time.

integral_constant<int, 3> i;        // ERROR integral_constant<int, 3> is not a type.
auto i = integral_constant<int, 3>; // OK: i is an int with the value 3.

1 2	integral_constant<int, 3> i; // ERROR integral_constant<int, 3> is not a type. auto i = integral_constant<int, 3>; // OK: i is an int with the value 3.

Variable templates can also be specialized:

template<size_t N>
constexpr size_t Fib = Fib<N-1> + Fib<N-2>;

template<>
constexpr size_t Fib<0> = 0;

template<>
constexpr size_t Fib<1> = 1;

template<size_t N>

constexpr size_t Fib = Fib<N-1> + Fib<N-2>;

template<>

constexpr size_t Fib<0> = 0;

template<>

constexpr size_t Fib<1> = 1;

The Fib variable template computes the N^th Fibonacci number.

std::cout << Fib<10> << std::endl;

1	std::cout << Fib<10> << std::endl;

This will print 55 to the console.

Variable templates can also be used as a limited form of type traits:

template<typename T>
constexpr bool is_integral = false;

template<>
constexpr bool is_integral<short> = true;

template<>
constexpr bool is_integral<int> = true;

template<>
constexpr bool is_integral<long> = true;

// ... specialized for all other integral types.

template<typename T>

constexpr bool is_integral = false;

template<>

constexpr bool is_integral<short> = true;

template<>

constexpr bool is_integral<int> = true;

template<>

constexpr bool is_integral<long> = true;

// ... specialized for all other integral types.

If T is an integral type then is_integral<T> is true. For all other types, is_integral<T> is false.

Type-traits are discussed in more detail later in the article.

Alias Template

Templates can be aliased using the using keyword:

template<typename T, T v>
constexpr T integral_constant = v;

template<bool v>
using bool_constant = integral_constant<bool, v>;

template<typename T, T v>

constexpr T integral_constant = v;

template<bool v>

using bool_constant = integral_constant<bool, v>;

On line 5, bool_constant is defined as an alias template of the integral_constant variable template where T is bool. The value v remains open as a non-type template parameter.

typename Keyword

Besides being used as the keyword used to introduce a type template parameter, the typename keyword is also used in a class or function template definition to declare that a type is dependent on a template parameter.

For example, suppose we have the following class template:

template<typename T>
struct MyClassTemplate
{
    using type = T;
};

template<typename T>

struct MyClassTemplate

{

using type = T;

};

The MyClassTemplate class template has a single template parameter (T) and type is a type alias of T.

Now suppose we have a function template that uses MyClassTemplate:

template<typename U>
U MyFuncTemplate(U a)
{
    MyClassTemplate<U>::type b; // ERROR: Use of dependent type must be prefixed with 'typename'
    b = a;
    return b;
}

template<typename U>

U MyFuncTemplate(U a)

{

MyClassTemplate<U>::type b; // ERROR: Use of dependent type must be prefixed with 'typename'

b = a;

return b;

}

The MyFuncTemplate function template has a single template parameter (U) and declares a local variable (b) whose type is MyClassTemplate<U>::type. Since MyClassTemplate<U>::type names a type and that type is dependent on the template parameter (U), then MyClassTemplate<U>::type must be proceeded by typename:

template<typename U>
U MyFuncTemplate(U a)
{
    typename MyClassTemplate<U>::type b; // OK: Use of dependent type is prefixed with 'typename'
    b = a;
    return b;
}

template<typename U>

U MyFuncTemplate(U a)

{

typename MyClassTemplate<U>::type b; // OK: Use of dependent type is prefixed with 'typename'

b = a;

return b;

}

The need for the typename keyword in this case, can be avoided by using an alias template:

template<typename T>
using MyClassTemplate_t = typename MyClassTemplate<T>::type;

template<typename U>
U MyFuncTemplate(U a)
{
    MyClassTemplate_t<U> b; // OK: MyClassTemplate_t names a type.
    b = a;
    return b;
}

template<typename T>

using MyClassTemplate_t = typename MyClassTemplate<T>::type;

template<typename U>

U MyFuncTemplate(U a)

{

MyClassTemplate_t<U> b; // OK: MyClassTemplate_t names a type.

b = a;

return b;

}

The typename keyword is used to name a type that is dependent on a template parameter unless it was already established as a type (by using a typedef or a (template) type alias.

Template Specialization

Both function templates and class templates can be specialized for specific types. When all template parameters are specialized, then it is called fully specialized. Suppose we have the following function template definition:

template<typename T, typename U>
auto add(T a, U b) -> decltype(a + b)
{
    return a + b;
}

template<typename T, typename U>

auto add(T a, U b) -> decltype(a + b)

{

return a + b;

}

The function template can be specialized by declaring the function with an empty template parameter list template<> and specifying the specialized template arguments after the function name:

template<>
double add<double, double>(double a, double b)
{
    return a + b;
}

template<>

double add<double, double>(double a, double b)

{

return a + b;

}

All occurrences of template parameters (T and U) in the function must also be replaced with the specialized template arguments (double).

It is possible to provide the same functionality by using function overloading:

double add(double a, double b)
{
    return a + b;
}

double add(double a, double b)

{

return a + b;

}

It is perfectly legal to overload function templates in this way.

The compiler will use the specialized (or overloaded) version of the function template if all of the substituted template arguments (either explicitly or implicitly) match the specialized version:

float a = add(3.0f, 4.0f); // Uses generic version.
double b = add(3.0, 4.0);  // Uses specialized version for doubles.

1 2	float a = add(3.0f, 4.0f); // Uses generic version. double b = add(3.0, 4.0); // Uses specialized version for doubles.

Similar to function templates, class templates can also be specialized. If we take the Array class template from the Class Template section and we want to specialize it for 4-component floating-point values:

template<>
class Array<float, 4>
{
public:
    Array()
    : m_Vec(_mm_setzero_ps())
    {}

    size_t size() const
    {
        return 4;
    }

    float& operator[](size_t i)
    {
        assert(i < 4);

        return m_Data[i];
    }

    const float& operator[](size_t i) const
    {
        assert(i < 4);

        return m_Data[i];
    }

private:
    union
    {
        __m128 m_Vec;     // Vectorized data.
        float  m_Data[4]; // Float data.
    };
};

template<>

class Array<float, 4>

{

public:

Array()

: m_Vec(_mm_setzero_ps())

{}

size_t size() const

{

return 4;

}

float& operator[](size_t i)

{

assert(i < 4);

return m_Data[i];

}

const float& operator[](size_t i) const

{

assert(i < 4);

return m_Data[i];

}

private:

union

{

__m128 m_Vec; // Vectorized data.

float m_Data[4]; // Float data.

};

The specialized version of the Array class template allows you to provide a different implementation of the class depending on its template arguments. In this case, we provide a specialization for Array<float, 4> that allows for some SSE optimizations to be made.

It is important to note that if you specialize a class template, you must also specialize all of the member functions of that class. This can be quite cumbersome for large classes, especially if you decide to refactor the generic class template, you must also update all specialized versions of the class.

Keep in mind that the compiler will only generate code for class template member functions that are used. That is, if you never call a specific member function of a specialized class template, then no code will be generated for that version of the member function. If a specialized class template defines a member function that just doesn’t make any sense for a certain specialized type, and you are sure that the member function is not being used anywhere in the codebase, then you can leave that function undefined in the specialized version of the class template.

Partial Specialization

Although it is not possible to partially specialize function templates, we can achieve something similar by using function template overloading. Let’s consider the max function template introduced in the previous section on Function Templates. Suppose we want to provide an implementation for pointer types:

template<typename T, typename U>
auto max(const T* a, const U* b) -> decltype(*a > *b ? *a : *b)
{
    return *a > *b ? *a : *b;
}

template<typename T, typename U>

auto max(const T* a, const U* b) -> decltype(*a > *b ? *a : *b)

{

return *a > *b ? *a : *b;

}

This version of the function template is used whenever pointers are used as the arguments to the function as in the following example:

double d = 3.0;
int i = 5;

auto k = max(&d, &i); // Uses double max(const double* a, const int* b);

double d = 3.0;

int i = 5;

auto k = max(&d, &i); // Uses double max(const double* a, const int* b);

Strictly speaking, this is not partial specialization because none of the template parameters are specialized. We’re just providing a specific implementation when the types exhibit specific characteristics.

Unlike function templates, class templates can be partially specialized. Special implementations of class templates can be created to handle specific situations. Consider the Array class template from before. A special implementation can be created if the array holds pointer types:

template<typename T, size_t N>
class Array<T*, N>
{
public:
    explicit Array(T* data)
        : m_Data(data)
    {}

    T& operator[](size_t i)
    {
        assert(i < N);

        return m_Data[i];
    }

    const T& operator[](size_t i) const
    {
        assert(i < N);

        return m_Data[i];
    }

private:
    T* m_Data;
};

template<typename T, size_t N>

class Array<T*, N>

{

public:

explicit Array(T* data)

: m_Data(data)

{}

T& operator[](size_t i)

{

assert(i < N);

return m_Data[i];

}

const T& operator[](size_t i) const

{

assert(i < N);

return m_Data[i];

}

private:

T* m_Data;

};

A class template can be partially specialized by specifying the template keyword followed by a list of template parameters surrounded by angle brackets, just as with the non-specialized class template. The specialized template parameters are specified after the class name (T* and N in this case).

This implementation of the Array class template will be used when T is a pointer type. This may not seem like a very useful thing, but now we have a class template that can provide all the functionality of the original Array class template, but instead of allocating a static array, it now works with arbitrary data that is allocated elsewhere.

float p[16] = {};
auto a = Array<float*, 16>(p);
// a provides all the functionality of Array on arbitrary data.
a[8] = 1.0f;

float p[16] = {};

auto a = Array<float*, 16>(p);

// a provides all the functionality of Array on arbitrary data.

a[8] = 1.0f;

Similarly to a fully specialized class template, if one of the template parameters is fully defined then it does not need to be listed in the template parameter list, but must be specified in the template argument list (after the class name):

// Specialized for arrays of size 4 and arbitrary type.
template<typename T>
class Array<T, 4>
{
    ...
};

// Specialized for float arrays of arbitrary size.
template<size_t N>
class Array<float, N>
{
    ...
};

// Specialized for arrays of size 4 and arbitrary type.

template<typename T>

class Array<T, 4>

{

...

};

// Specialized for float arrays of arbitrary size.

template<size_t N>

class Array<float, N>

{

...

};

Partial template specialization is the cornerstone of type traits and SFINAE.

Variadic Templates

Variadic templates are function templates or class templates that can accept an unbounded number of template arguments.

For example, suppose we want a function that creates an std::unique_ptr from an arbitrary type:

template<typename T, typename... Args>
std::unique_ptr<T> make_unique(Args&&... args)
{
    return std::unique_ptr<T>(new T(std::forward<Args>(args)...));
}

template<typename T, typename... Args>

std::unique_ptr<T> make_unique(Args&&... args)

{

return std::unique_ptr<T>(new T(std::forward<Args>(args)...));

}

For some reason, std::make_shared was introduced in C++11 but std::make_unique wasn’t introduced until C++14. This example provides a possible implementation of std::make_unique for C++11 compilers.

There are a few things to note here:

The template parameter list contains a template parameter pack in the form of typename... Args
An arbitrary number of arguments are passed to the function in the form of Args&&.... Not to be mistaken by an rvalue reference, this is called a forwarding reference which preserves the value category of the function arguments when used in conjunction with std::forward
The arguments are unpacked by performing a pack expansion which replaces the parameter pack by a comma-separated list of the arguments using the pattern immediately preceding the ... (ellipsis)

For example, suppose we have the following class:

class Object
{
public:
    Object(int i, float f, int* ip, double d)
    : m_i(i)
    , m_f(f)
    , mp_i(ip)
    , m_d(d)
    {}

private:
    int m_i;
    float m_f;
    int* mp_i;
    double m_d;
};

class Object

{

public:

Object(int i, float f, int* ip, double d)

: m_i(i)

, m_f(f)

, mp_i(ip)

, m_d(d)

{}

private:

int m_i;

float m_f;

int* mp_i;

double m_d;

};

And if the make_unique function template was invoked with:

int i = 3;
float f = 4.0f;
double d = 6.0;

auto o = make_unique<Object>(i, f, &i, d);

int i = 3;

float f = 4.0f;

double d = 6.0;

auto o = make_unique<Object>(i, f, &i, d);

Then the make_unique function would generate something like this:

std::unique_ptr<Object> make_unique(int args0, float args1, int* args2, double args3)
{
    return std::unique_ptr<Object>(new Object(std::forward<int>(args0), std::forward<float>(args1), std::forward<int*>(args2), std::forward<double>(args3)));
}

std::unique_ptr<Object> make_unique(int args0, float args1, int* args2, double args3)

{

return std::unique_ptr<Object>(new Object(std::forward<int>(args0), std::forward<float>(args1), std::forward<int*>(args2), std::forward<double>(args3)));

}

Recursive Variadic Templates

Suppose you want to write a function that prints an arbitrary number of arguments to the standard output stream. Using a C++17 compiler, this can be accomplished using fold expressions:

template<typename... Args>
void print(Args... args)
{
    (std::cout << ... << args) << std::endl;
}

template<typename... Args>

void print(Args... args)

{

(std::cout << ... << args) << std::endl;

}

But how could this be accomplished without a C++17 compiler? To accomplish this without fold expressions, we need to create a recursive template function. To do this we must:

Define the base case (only a single template parameter)
Define the recursive case (where multiple template parameters are passed in a parameter pack)

First, let’s define the case where only a single argument is passed:

template<typename Arg>
void print(Arg arg)
{
    std::cout << arg << std::endl;
}

template<typename Arg>

void print(Arg arg)

{

std::cout << arg << std::endl;

}

And the recursive case with a parameter pack:

template<typename Arg, typename... Args>
void print(Arg arg, Args... args)
{
    std::cout << arg;
    print(args...);
}

template<typename Arg, typename... Args>

void print(Arg arg, Args... args)

{

std::cout << arg;

print(args...);

}

The subtle trick here is that the recursive case has two template parameters:

typename Arg
typename... Args

This way, the first argument can be extracted from the parameter pack and the rest of the arguments are passed to the recursive print function. When there is only a single argument left in the parameter pack, the base case (with a single template argument) is used.

At this point, you should have a pretty good idea of how to use templates in your code. In the following sections, I will show a few more complex uses of templates.

Template Type Deduction

Template type deduction is the process the compiler performs to determine the type that is used to instantiate a function or class template. Many programmers use templates with a reasonable amount of success without really understanding how template type deduction works. This might be sufficient for simple use cases but becomes complicated (and perhaps unintuitive) in more complex applications of templates.

Understanding template type deduction forms the foundation for understanding how the decltype specifier works.

Scott Meyers provides a very good explanation of how type deduction works^[7]. I will attempt to summarize Scott Meyers’ explanation here.

As we’ve seen in previous examples, function templates have the following basic form:

template <typename T>
void f(ParamType param);

1 2	template <typename T> void f(ParamType param);

In the snippet above, T and ParamType may be different in the case that ParamType has modifiers (const, pointer (*), or reference (&) qualifiers). For example, if the template is declared like this:

template<typename T>
void f(const T& param); // ParamType is const T&

1 2	template<typename T> void f(const T& param); // ParamType is const T&

Now suppose the template function is invoked like this:

int x = 0;
f(x); // Call f with an int (lvalue)

1 2	int x = 0; f(x); // Call f with an int (lvalue)

In this case, T is deduced to int and ParamType is deduced to const int&.

In this case, it seems obvious that T is deduced to int since f was invoked with an int argument, but it’s not always that obvious. The type deduced for T is dependent on not only the argument type, but also the form of ParamType. There are three forms of ParamType that must be considered:

ParamType is a pointer or reference type, but not a forwarding reference
ParamType is a forwarding reference
ParamType is neither a pointer nor a reference

Scott Meyers uses the term universal reference to refer to the double ampersand (&&) being applied to template parameters (not to be mistaken with rvalue references). Since the C++ standard uses the term forwarding reference, I will use that term in this article.

A forwarding reference is a special kind of reference that preserve the value category of a (function) argument making it possible to forward it to another function using std::forward.

For each of the three cases, consider the general form of invoking the template function:

template <typename T>
void f(ParamType param);

f(expr);  // Deduce T and ParamType from expr.

template <typename T>

void f(ParamType param);

f(expr); // Deduce T and ParamType from expr.

Case 1: ParamType is a Reference or Pointer

In the first case, ParamType is a reference or pointer type, but not a forwarding reference. In this case, type deduction works like this:

If expr evaluates to a reference, ignore the reference part.
Then match expr‘s type against ParamType to determine T.

For example, if the function template is declared like this:

template<typename T>
void f(T& param); // param is a reference.

1 2	template<typename T> void f(T& param); // param is a reference.

Then given the following variables:

int i          = 3; // i is an int.
const int ci   = i; // ci is a const int.
const int& rci = i; // rci is a reference to a const int.

f(i);   // T is int, param's type is int&
f(ci);  // T is const int, param's type is const int&
f(rci); // T is const int, param's type is const int&

int i = 3; // i is an int.

const int ci = i; // ci is a const int.

const int& rci = i; // rci is a reference to a const int.

f(i); // T is int, param's type is int&

f(ci); // T is const int, param's type is const int&

f(rci); // T is const int, param's type is const int&

Notice on lines 6, and 7 where expr is a const int or const int&, then T is deduced to be const int. The constness of expr becomes part of the type deduced for T.

If, on the other hand, ParamType is changed to const T& then type deduction works slightly differently:

template<typename T>
void f(const T& param); // param is now a reference to const T.

int i          = 3; // i is an int.
const int ci   = i; // ci is a const int.
const int& rci = i; // rci is a reference to a const int.

f(i);   // T is int, param's type is const int&
f(ci);  // T is int, param's type is const int&
f(rci); // T is int, param's type is const int&

template<typename T>

void f(const T& param); // param is now a reference to const T.

int i = 3; // i is an int.

const int ci = i; // ci is a const int.

const int& rci = i; // rci is a reference to a const int.

f(i); // T is int, param's type is const int&

f(ci); // T is int, param's type is const int&

f(rci); // T is int, param's type is const int&

Since the constness is now part of param‘s type, there is no need for const to be part of T‘s type deduction.

If param were a pointer or a pointer to const, then the type deduction for T works the same way:

template<typename T>
void f(T* param); // param is now a pointer to T.

int i         = 3;  // i is an int.
const int* pi = &i; // pi is a pointer to const int.

f(&i); // T is int, param's type is const int*
f(pi); // T is const int, param's type is const int*

template<typename T>

void f(T* param); // param is now a pointer to T.

int i = 3; // i is an int.

const int* pi = &i; // pi is a pointer to const int.

f(&i); // T is int, param's type is const int*

f(pi); // T is const int, param's type is const int*

This may seem obvious so far, but becomes less obvious if ParamType is a forwarding reference.

Case 2: ParamType is a Forwarding Reference

Now let’s consider the case where ParamType is a forwarding reference:

template<typename T>
void f(T&& param); // param is now a forwarding reference.

int i          = 3; // i is an int (lvalue).
const int ci   = i; // ci is a const int (lvalue).
const int& rci = i; // rci is a reference to a const int (lvalue).

f(i);   // T is int&, param's type is also int&
f(ci);  // T is const int&, param's type is also const int&
f(rci); // T is const int&, param's type is also const int&
f(3);   // T is int, param's type is int&&

template<typename T>

void f(T&& param); // param is now a forwarding reference.

int i = 3; // i is an int (lvalue).

const int ci = i; // ci is a const int (lvalue).

const int& rci = i; // rci is a reference to a const int (lvalue).

f(i); // T is int&, param's type is also int&

f(ci); // T is const int&, param's type is also const int&

f(rci); // T is const int&, param's type is also const int&

f(3); // T is int, param's type is int&&

On line 4, an int variable (i) is defined. This is an lvalue (according to the value category rules defined at the beginning of this article). On line 9, i is passed to f. In this case, ParamType is deduced to int& (lvalue reference) and T is deduced to int& (lvalue reference).

On line 9, ci (lvalue) is passed to f and ParamType is deduced to const int& (lvalue reference) and T is deduced to const int& (lvalue reference). Similar deduction rules are applied to rci on line 10.

On line 11, the value 3 (prvalue, which is a primary value category of rvalue) is passed to f. In this case ParamType is deduced to int&& (rvalue reference) and T is deduced to int. The deduction rules for rvalues are the same as Case 1 above (expr‘s type is matched against ParamType to determine T).

The general rules of type deduction when ParamType is a forwarding reference, are:

If expr is an lvalue, both T and ParamType are deduced to be lvalue references.
If expr is a rvalue (prvalue or xvalue), then the rules for Case 1 are applied.

In short, use a forwarding reference when you need to maintain the value category of the template argument. This is almost always the case when the arguments are being forwarded to another function.

Case 3: ParamType is Neither a Pointer nor a Reference

If ParamType is neither a pointer nor a reference, then we say that the parameter is passed-by-value:

template<typename T>
void f(T param); // param is now passed-by-value.

1 2	template<typename T> void f(T param); // param is now passed-by-value.

In this case, the rules for type deduction are:

If expr‘s type is a reference, ignore the reference part
If expr‘s type is const, ignore that too.

Then we have:

int i          = 3; // i is an int.
const int ci   = i; // ci is a const int.
const int& rci = i; // rci is a reference to a const int.

f(i);   // T is int, param's type is also int
f(ci);  // T is int, param's type is also int
f(rci); // T is int, param's type is also int

int i = 3; // i is an int.

const int ci = i; // ci is a const int.

const int& rci = i; // rci is a reference to a const int.

f(i); // T is int, param's type is also int

f(ci); // T is int, param's type is also int

f(rci); // T is int, param's type is also int

Note that despite ci and rci being const values, param doesn’t become const. Just becase expr can’t be modified doesn’t mean that a copy of it can’t be.

This pretty much summarizes the rules that are applied during template parameter type deduction. There are a few more cases that can be considered, for example how static arrays and function objects decay to their pointer types (see the decay type trait for more information). I encourage the reader to consult Scott Meyers’ books^[7] for more information regarding the edge cases of template parameter type deductions. But at this point, you should have a good foundation for understanding the decltype specifier and std::declval which is the subject of the next sections.

decltype Specifier

The decltype specifier is used to inspect the declared type and value category of an expression.

Earlier, in the section about Function Templates, the decltype specifier was used to determine the return type for the max function template. If you read the warning that followed the code example, you might know that in certain cases, the compiler will generate a warning about returning a reference to a temporary. But under what circumstances does this happen?

In most cases, the decltype produces the expected type:

int h        = 0;
int* i       = &h;
int& j       = h;
const int k  = 0;
const int* l = &k;
const int& m = k; 

decltype(h) n = 0;  // n is int
decltype(i) o = &n; // o is int*
decltype(j) p = n;  // p is int&
decltype(k) q = 0;  // p is const int
decltype(l) r = &q; // r is const int*
decltype(m) s = q;  // s is const int&

int h = 0;

int* i = &h;

int& j = h;

const int k = 0;

const int* l = &k;

const int& m = k;

decltype(h) n = 0; // n is int

decltype(i) o = &n; // o is int*

decltype(j) p = n; // p is int&

decltype(k) q = 0; // p is const int

decltype(l) r = &q; // r is const int*

decltype(m) s = q; // s is const int&

No surprises here. decltype gives the exact type as the provided expression maintaining const (and volatile), reference (&) and pointer (*) attributes.

When the the expression passed to decltype is parenthesized, then the expression is treated as an lvalue and decltype adds a reference to the expression:

int h        = 0;
int* i       = &h;
int& j       = h;
const int k  = 0;
const int* l = &k;
const int& m = k; 

decltype((h)) n = h; // n is int&
decltype((i)) o = i; // o is int*&
decltype((j)) p = j; // p is int&
decltype((k)) q = k; // q is const int&
decltype((l)) r = l; // r is const int*&
decltype((m)) s = m; // s is const int&

int h = 0;

int* i = &h;

int& j = h;

const int k = 0;

const int* l = &k;

const int& m = k;

decltype((h)) n = h; // n is int&

decltype((i)) o = i; // o is int*&

decltype((j)) p = j; // p is int&

decltype((k)) q = k; // q is const int&

decltype((l)) r = l; // r is const int*&

decltype((m)) s = m; // s is const int&

Okay, but this doesn’t explain why the max function template can sometimes return a reference. To understand when this happens, we need to look at the deduction guide for the ternary (conditional) operator. The ternary operator has the form:

condition ? expr1 : expr2

1	condition ? expr1 : expr2

First, condition is evalutated and (implicitly converted) to bool. If the result is true, then expr1 is evaluated. If the result is false, then expr2 is evaluated. The deduction rules for the resulting value of the ternary operator are complex and you can read the full guide here.

One of the rules of the deduction guide for the ternary operator states that if expr1 and expr2 are glvalues (lvalues or xvalues) of the the same type and the same value category, then the result has the same type and value category.

Here is the max function template again:

template<typename T, typename U>
auto max(T a, U b) -> decltype(a > b ? a : b)
{
    return a > b ? a : b;
}

template<typename T, typename U>

auto max(T a, U b) -> decltype(a > b ? a : b)

{

return a > b ? a : b;

}

So if T and U are the same type and value category (see Case 3 above when the template parameter is passed-by-value) then decltype(a > b ? a : b) will have the same type and value category of both a and b. If both a and b are the same type and they are always both lvalues (since they are identified by a name), then in order to avoid creating a temporary, decltype(a > b ? a : b) results in an lvalue references that refers to either a or b (whichever is larger).

Let’s take a look at a few examples of this:

int a = 3;
int b = 5;
double c = 3.0;
double d = 5.0;

decltype(a > b ? a : b) g; // g is int&
decltype(a > c ? a : c) h; // h is double
decltype(c > d ? c : d) i; // i is double&
decltype(3 > 5 ? 3 : 5) k; // k is int

int a = 3;

int b = 5;

double c = 3.0;

double d = 5.0;

decltype(a > b ? a : b) g; // g is int&

decltype(a > c ? a : c) h; // h is double

decltype(c > d ? c : d) i; // i is double&

decltype(3 > 5 ? 3 : 5) k; // k is int

On line 6, both a and b are ints and they are both lvalues. The result of the ternary operator is an lvalue reference.

On line 7, a is an int and c is a double. In this case, they are not the same type and the result of the ternary operator is the the type of the widest operand (in this case, double)

On line 8, both c and d are doubles and they are both lvalues. The result of the tenary operator is an lvalue reference.

On line 9, both operands are prvalues of type int. In this case, the result of the ternary operator is also a prvalue.

Consequently, the result of the ternary operator has an interesting side effect that you should be aware of. You can sometimes assign a value to the result of the ternary operator:

int a = 3;
int b = 5;

( a > b ? a : b ) = 10; // OKAY, b now has the value 10.
( 3 > b ? 3 : b ) = 10; // ERROR: expression must be a modifiable lvalue.
( 3 > 5 ? 3 : 5 ) = 10; // ERROR: expression must be a modifiable lvalue.

int a = 3;

int b = 5;

( a > b ? a : b ) = 10; // OKAY, b now has the value 10.

( 3 > b ? 3 : b ) = 10; // ERROR: expression must be a modifiable lvalue.

( 3 > 5 ? 3 : 5 ) = 10; // ERROR: expression must be a modifiable lvalue.

In the case where the the result of the ternary operator is an lvalue reference, you can actually assign a value to that result. In all other cases, the result of the ternary operator is a temporary prvalue that can’t be modified directly (unless it is stored in a lvalue first).

Okay, you’ve probably heard enough about the ternary operator. This should be enough knowledge to know under which circumstance the max function template returns a reference, but how can we fix this? In later sections, I’ll talk about using type traits to coerce declval to give us what we want. But before we get to type traits, there is one more tool we need in our template toolbox, and that’s the std::declval.

std::declval()

std::declval is a utility function that converts any type to a reference type without the need to create an instance of an object.

Okay, maybe that doesn’t help to understand why we need std::declval, so let’s take a look at an example. Suppose we have an abstract base class:

struct Abstract
{
    virtual ~Abstract() = default;
    virtual int value() const = 0;
};

struct Abstract

{

virtual ~Abstract() = default;

virtual int value() const = 0;

};

We know that Abstract is an abstract type because it declares at least one pure virtual function. Pure virtual functions are not required to (but may) have a definition. Classes with pure virtual functions are called abstract classes and cannot be instantiated.

Now suppose we wanted to determine the type that is returned from the Abstract::value method. As explained in the previous section, we can use the decltype keyword for this:

decltype(Abstract().value()) a; // ERROR: cannot instantiate abstract class.
decltype(Abstract::value()) b;  // ERROR: illegal call of non-static member function.
decltype(std::declval<Abstract>().value()) c; // OK: c is type int.

decltype(Abstract().value()) a; // ERROR: cannot instantiate abstract class.

decltype(Abstract::value()) b; // ERROR: illegal call of non-static member function.

decltype(std::declval<Abstract>().value()) c; // OK: c is type int.

On line 10, we try to to determine the return type by constructing an instance of Abstract and inspect the return value of the value method. In this case, the compiler complains since, as was previously established, Abstract is an abstract class and can’t be instantiated (even in unevaluated expression like the decltype operator).

On line 11, we try to determine the return value by using a scope resolution operator (::). This only works if Abstract::value is a static function.

On line 12, the std::declval function template allows for the use of non-static member functions of abstract base classes, (or with types with deleted or private constructors, which is common when dealing with singletons) without requiring an instance of the type.

The std::declval utility function can be implemented like this:

template<typename T>
typename std::add_rvalue_reference<T>::type declval() noexcept;

1 2	template<typename T> typename std::add_rvalue_reference<T>::type declval() noexcept;

We haven’t looked at type traits yet, but I think you can guess that std::add_rvalue_reference<T> makes T an rvalue reference.

You may have noticed that the declval function template only provides a declaration but not a definition. This is no mistake. This function does not have a definition! It simply converts T to an rvalue reference so that it can be used in an unevaluated context such as decltype.

std::declval converts any type (T) to a reference type to enable the use of member functions without the need to construct an instance of T.

Since std::declval is not defined and therefore, it can only be used in an unevaluated context such as decltype.

Type Traits

C++11 introduces the type_traits library.

Type traits defines a compile-time template-based interface to query or modify the properties of types.

Type traits allow you to discover certain things about a type at compile-time. Some things you may want to know about types are:

Is it an integral type?
Is it a floating-point type?
Is it a class type?
Is it a function type?
Is it a pointer type?
Are two types the same?
Is one type derived from the other?
Is one type convertible to another?

And the list goes on… There are many things we might want to know about one or more types that can be determined at compile-time.

Don’t confuse type traits with Run-Time Type Information (RTTI) which is used to query type information at run-time. Type traits are resolved at compile-time and impose no run-time overhead.

Type traits are the cornerstone for “Substitution Failure Is Not An Error” (SFINAE). But before we look at SFINAE, let’s investigate a few type traits that we can use as the basis for SFINAE later.

Keep in mind that a lot of the type traits described in following sections comes from the Standard Template Library (STL). You don’t need to define these types yourself in your own code. You can find the original source code for the type_traits library here:

Microsoft STL: https://github.com/microsoft/STL
GCC: https://github.com/gcc-mirror/gcc
Clang/LLVM: https://github.com/llvm/llvm-project

My motivation for describing the type traits in this article is to give the reader a better understanding of how they work. Once you know how they work, you will have a better understanding of how to use them correctly.

integral_constant

The integral_constant structure is the base class for the type traits library. It is a wrapper for a static constant of a specified type. It wraps both the type and a value in a struct so it can be used as a type. You’ll see why this is useful later.

template<typename T, T v>
struct integral_constant
{
    // Member types
    using value_type = T;
    using type = integral_constant;

    // Member constants
    static constexpr T value = v;

    // Member functions
    constexpr operator value_type() const noexcept
    {
        return value;
    }

    constexpr value_type operator()() const noexcept
    {
        return value;
    }
};

template<typename T, T v>

struct integral_constant

{

// Member types

using value_type = T;

using type = integral_constant;

// Member constants

static constexpr T value = v;

// Member functions

constexpr operator value_type() const noexcept

{

return value;

}

constexpr value_type operator()() const noexcept

{

return value;

}

};

The integral_constant class (struct) template is composed of a type template parameter (T) and a non-type template parameter v (of type T).

The value type that was used to instantiate the integral_constant can be queried through the value_type type alias and the type of the integral_constant itself can be queried through the type type alias.

The operator value_type() member function defined on line 12 is an implicit conversion operator which allows an instance of the integral_constant template to be converted to value_type at compile-time. This allows an instance of integral_constant to be used in place where value_type is expected (in mathematical expressions for example).

The value_type operator() member function defined on line 17 is a function call operator that takes no parameters and returns value. This allows integral_constant to be used as a function object that takes no parameters and returns the stored value.

using three_t = integral_constant<int, 3>;
using five_t = integral_constant<int, 5>;

three_t three;
five_t five;

auto fifteen = three_t() * five_t();
fifteen = three * five;

std::cout << "3 * 5 = " << fifteen << std::endl;

using three_t = integral_constant<int, 3>;

using five_t = integral_constant<int, 5>;

three_t three;

five_t five;

auto fifteen = three_t() * five_t();

fifteen = three * five;

std::cout << "3 * 5 = " << fifteen << std::endl;

On lines 1 and 2, two type aliases of the integral_constant template are defined: three_t which is a type that represents 3, and five_t which is a type that represents 5.

On lines 4 and 5, two instances are instantiated using the type aliases that were just defined. three is an instance of type_constant<int, 3> and five is an instance of type_constant<int, 5>.

On line 7 and 8, two different methods to get the internal value are demonstrated. The first method on line 7 uses the function call operator to retrieve the internal value. On line 8, the implicit conversion operator is used to convert three and five to their integer equivalents to be multiplied together. Both expressions result in 15. If you run this program, the following is printed to the console:

3 * 5 = 15

That might be the most contrived method of computing the value 15 I’ve ever seen, but in the next section it will be become clear why this is useful.

bool_constant

With the definition of integral_constant from the previous section, other types can be derived from integral_constant. One useful type that can be derived from integral_constant is bool_constant. It is not necessary to define a full class for this as a template alias will do:

template<bool v>
using bool_constant = integral_constant<bool, v>;

1 2	template<bool v> using bool_constant = integral_constant<bool, v>;

The bool_constant defines a “boolean” integral_constant. And as you may have guessed, we can define two new types based on bool_constant.

true_type

true_type is a type alias of bool_constant with a value of true:

using true_type = bool_constant<true>;

1	using true_type = bool_constant<true>;

false_type

false_type is a type alias of bool_constant with a value of false:

using false_type = bool_constant<false>;

1	using false_type = bool_constant<false>;

Both true_type and false_type are aliases of integral_type which means that they can be used wherever a class or struct type can be used. For example, we can create a partial specialization of a class that is derived from either true_type or false_type. But before I get into that, I need to introduce another useful tool for our type traits library: enable_if.

type_identity

At first glance, the type_identity class template may not seem very useful. It simply mimics the type T that was specified in the template argument.

template<class T>
struct type_identity
{
    using type = T;
};

template<class T>
using type_identity_t = typename type_identity<T>::type;

template<class T>

struct type_identity

{

using type = T;

};

template<class T>

using type_identity_t = typename type_identity<T>::type;

The type_identity class template becomes useful in a non-deduced context (for example when used with the decltype specifier). We’ll use it later to help form SFINAE enabled types (see add_lvalue_reference and add_rvalue_reference).

void_t

void_t is an alias template that maps any number of type template parameters to void. This is useful in the context of SFINAE where you only want to check if a certain set of operations is valid on a type but you don’t care about the return type of that check. void_t allows you to form these expressions without concern for the return type.

template<class... T>
using void_t = void;

1 2	template<class... T> using void_t = void;

The void_t alias template is commonly used to check if a certain operation is valid on a specific type. For example, if we want to check if a type supports the pre-increment operator, but we don’t care about the the actual result type, then we could do something like this:

template<class, class = void>
struct has_pre_increment_operator : false_type
{};

template<class T>
struct has_pre_increment_operator<T, void_t<decltype(++std::declval<T&>())>> : true_type
{};

template<class, class = void>

struct has_pre_increment_operator : false_type

{};

template<class T>

struct has_pre_increment_operator<T, void_t<decltype(++std::declval<T&>())>> : true_type

{};

In this example, the primary template for has_pre_increment_operator is derived from false_type. The primary template is only chosen if there isn’t a partial specialization that is a better match. In order to get the compiler to choose the specialized version of the template definition, the operation ++std::declval<&T>() must succeed. But since we only want to see if the operation succeeded, but we don’t care what the return value is, we can wrap the result of performing the pre-increment operator in the void_t alias template.

Since void_t takes a variadic number of template parameters, void_t can be used to check if any number of operations are valid on one or more types.

When the compiler fails to instantiate the second template argument in the specialized version of the has_pre_increment_operator, this is called substitution failure and is the basis of SFINAE (Substitution Failure Is Not An Error). SFINAE is used to express type trait operations and the void_t template alias is used to help formulate those expressions.

enable_if

The enable_if struct template provides a convenient mechanism to leverage SFINAE in our template classes. “Substitution Failure Is Not An Error” (or SFINAE) is a C++ technique to conditionally remove specific functions from overload resolution based on a type’s traits. We’ll get into more details of SFINAE later, for now let’s take a look at how we can define the enable_if template:

template<bool B, class T = void>
struct enable_if
{};

template<class T>
struct enable_if<true, T>
{
    using type = T;
};

template<bool B, class T = void>

struct enable_if

{};

template<class T>

struct enable_if<true, T>

{

using type = T;

};

The primary template for enable_if is a class template that has two template parameters:

bool B: A non-type template parameter that can be either true or false.
class T: A type template parameter that can be any type. If no type is provided, void is used by default.

The magic trick comes from the partial specialization that is defined when B is true. The type type alias is not defined in the primary template and is only defined when B is true. Any attempt to access the type type alias when B is false will fail (since it’s just not defined in this case).

We’ll see how we can use this to leverage SFINAE later. Before we can do that, we’ll need some type trait templates to work with.

To simplify coding, we’ll also define a helper template alias for the enable_if template:

template<bool B, class T = void>
using enable_if_t = typename enable_if<B, T>::type;

1 2	template<bool B, class T = void> using enable_if_t = typename enable_if<B, T>::type;

Now, instead of typing typename enable_if<B, T>::type, we only need to type enable_if_t<B, T>. As you can see, this saves us a lot of typing.

The enable_if_t template alias was introduced in C++14 but there is nothing stopping you from defining these kinds of template aliases in your C++11 code.

remove_const

Sometimes is it convenient to express a type without the const qualifier associated with it. The remove_const class template allows us to do just that:

template<class T>
struct remove_const
{
    using type = T;
};

template<class T>
struct remove_const<const T>
{
    using type = T;
};

template<class T>

struct remove_const

{

using type = T;

};

template<class T>

struct remove_const<const T>

{

using type = T;

};

The primary template for remove_const is only used when T is a non-const type. If T is const, then the partial specialization kicks-in to remove the const modifier from T.

And again, we’ll also define a helper template alias:

template<class T>
using remove_const_t = typename remove_const<T>::type;

1 2	template<class T> using remove_const_t = typename remove_const<T>::type;

The remove_const class template only removes the topmost const qualifier from T.

remove_volatile

Similar to remove_const, the remove_volatile class template can be used to remove the volatile qualifier from a type:

template<class T>
struct remove_volatile
{
    using type = T;
};

template<class T>
struct remove_volatile<volatile T>
{
    using type = T;
};

template<class T>

struct remove_volatile

{

using type = T;

};

template<class T>

struct remove_volatile<volatile T>

{

using type = T;

};

And the helper template alias:

template<class T>
using remove_volatile_t = typename remove_volatile<T>::type;

1 2	template<class T> using remove_volatile_t = typename remove_volatile<T>::type;

remove_cv

The remove_cv class template is used to remove the topmost const, volatile, or both qualifiers if present:

template<class T>
struct remove_cv
{
    using type = remove_const_t<remove_volatile_t<T>>;
};

// Helper template alias.
template<class T>
using remove_cv_t = typename remove_cv<T>::type;

template<class T>

struct remove_cv

{

using type = remove_const_t<remove_volatile_t<T>>;

};

// Helper template alias.

template<class T>

using remove_cv_t = typename remove_cv<T>::type;

In this example, the remove_const and remove_volatile are combined on line 4 to remove both const and volatile qualifiers from T (if present).

remove_reference

The remove_reference class template is used to remove any reference (or rvalue references) from a type.

template<class T>
struct remove_reference
{
    using type = T;
};

template<class T>
struct remove_reference<T&>
{
    using type = T;
};

template<class T>
struct remove_reference<T&&>
{
    using type = T;
};

// Helper template alias.
template<class T>
using remove_reference_t = typename remove_reference<T>::type;

template<class T>

struct remove_reference

{

using type = T;

};

template<class T>

struct remove_reference<T&>

{

using type = T;

};

template<class T>

struct remove_reference<T&&>

{

using type = T;

};

// Helper template alias.

template<class T>

using remove_reference_t = typename remove_reference<T>::type;

If T is a reference (or rvalue reference) type, then the remove_reference class template will strip off the reference from the type.

remove_cvref

Now we can combine remove_cv and remove_reference to remove const, volatile, and references from a type:

template<class T>
struct remove_cvref
{
    using type = remove_cv_t<remove_reference_t<T>>;
};

template<class T>
using remove_cvref_t = typename remove_cvref<T>::type;

template<class T>

struct remove_cvref

{

using type = remove_cv_t<remove_reference_t<T>>;

};

template<class T>

using remove_cvref_t = typename remove_cvref<T>::type;

remove_extent

It might be useful to extract the type of an array. The remove_extent class template can be used to extract the type of an array. For example, if T is an (bounded or unbounded) array of type X, then remove_extent_t<T> evaluates to X.

template<class T>
struct remove_extent 
{
    using type = T;
};

template<class T>
struct remove_extent<T[]> 
{
    using type = T;
};

template<class T, std::size_t N>
struct remove_extent<T[N]> 
{
    using type = T;
};

template<class T>

struct remove_extent

{

using type = T;

};

template<class T>

struct remove_extent<T[]>

{

using type = T;

};

template<class T, std::size_t N>

struct remove_extent<T[N]>

{

using type = T;

};

The primary template (lines 1-5) is used if T is not an array type. If T is an unbounded array (lines 7-11) or a bounded array (lines 13-17), then remove_extent<T>::type is defined to be the type of the array with the extents removed.

If T is a multidimensional array, remove_extent<T> only removes the first dimension.

A short-hand for the remove_extent class template:

template<typename T>
using remove_extent_t = typename remove_extent<T>::type;

1 2	template<typename T> using remove_extent_t = typename remove_extent<T>::type;

remove_all_extents

Since the remove_extent class template only removes the first dimension of multidimensional arrays, the remove_all_extents class template can be used to remove all of the extents of multidimensional arrays.

template<class T>
struct remove_all_extents
{
    using type = T;
};

template<class T>
struct remove_all_extents<T[]>
{
    using type = typename remove_all_extents<T>::type;
};

template<class T, std::size_t N>
struct remove_all_extents<T[N]>
{
    using type = typename remove_all_extents<T>::type;
};

template<class T>

struct remove_all_extents

{

using type = T;

};

template<class T>

struct remove_all_extents<T[]>

{

using type = typename remove_all_extents<T>::type;

};

template<class T, std::size_t N>

struct remove_all_extents<T[N]>

{

using type = typename remove_all_extents<T>::type;

};

The primary template (lines 1-5) for the remove_all_extents class template looks similar to the remove_extent class template. The primary template is only used when T is not an array type or all of the extents have already been removed from the type.

If T is an unbounded (line 7-11) or bounded (line 13-17) array type, then the appropriate partial specialization is used. In this case, the first dimension is removed from T and the remove_all_extents class template is invoked recursively to remove the next extent. This process continues until the primary template is reached.

And the shorthand form:

template<class T>
using remove_all_extents_t = typename remove_all_extents<T>::type;

1 2	template<class T> using remove_all_extents_t = typename remove_all_extents<T>::type;

remove_pointer

The remove_pointer class template can be used to remove the pointer from a type. Any const or volatile qualifiers added to the pointer are also removed.

Any const or volatile qualifiers added to the pointed-to type are not removed. For example, const int* becomes const int, but int* const becomes int and const int* const becomes const int. If you also want to remove the const or volatile qualifiers from the pointed-to type, then you must use the remove_cv class template as well.

template<class T>
struct remove_pointer
{
    using type = T;
};

template<class T>
struct remove_pointer<T*>
{
    using type = T;
};

template<class T>
struct remove_pointer<T* const>
{
    using type = T;
};

template<class T>
struct remove_pointer<T* volatile>
{
    using type = T;
};

template<class T>
struct remove_pointer<T* const volatile>
{
    using type = T;
};

template<class T>

struct remove_pointer

{

using type = T;

};

template<class T>

struct remove_pointer<T*>

{

using type = T;

};

template<class T>

struct remove_pointer<T* const>

{

using type = T;

};

template<class T>

struct remove_pointer<T* volatile>

{

using type = T;

};

template<class T>

struct remove_pointer<T* const volatile>

{

using type = T;

};

The primary template (lines 1-5) is used if T is not a pointer type. Partial specializations (lines 7-29) are used if T is a (const or volatile qualified) pointer type.

And a short-hand version:

template<class T>
using remove_pointer_t = typename remove_pointer<T>::type;

1 2	template<class T> using remove_pointer_t = typename remove_pointer<T>::type;

add_const

In some cases, you may want to add the const qualifier to a type. The add_const class template can be used to add the const qualifier to any type T (except for function and reference types, since these can’t be const qualified).

#pragma warning(push)
#pragma warning(disable: 4180) // Disable C4180: qualifier applied to function type has no meaning; ignored
template<class T>
struct add_const
{
    using type = const T;
};
#pragma warning(pop)

template<class T>
using add_const_t = typename add_const<T>::type;

#pragma warning(push)

#pragma warning(disable: 4180) // Disable C4180: qualifier applied to function type has no meaning; ignored

template<class T>

struct add_const

{

using type = const T;

};

#pragma warning(pop)

template<class T>

using add_const_t = typename add_const<T>::type;

Due to const collapsing rules, if T is already const, then adding another const to T does not change the constness of T.

If we try to apply the add_const class template to a function type, then the compiler will generate a C4180 warning that applying a const to a function type does not make sense and has no meaning. #pragma warning(disable: 4180) causes this warning to be suppressed in Visual Studio.

add_volatile

Similar to add_const class template, the add_volatile class template can be used to add the volatile qualifier to a type (except for function and reference types, since these can’t be volatile qualified).

#pragma warning(push)
#pragma warning(disable: 4180) // Disable C4180: qualifier applied to function type has no meaning; ignored
template<class T>
struct add_volatile
{
    using type = volatile T;
};
#pragma warning(pop)

template<class T>
using add_volatile_t = typename add_volatile<T>::type;

#pragma warning(push)

#pragma warning(disable: 4180) // Disable C4180: qualifier applied to function type has no meaning; ignored

template<class T>

struct add_volatile

{

using type = volatile T;

};

#pragma warning(pop)

template<class T>

using add_volatile_t = typename add_volatile<T>::type;

Similar to the add_const class template, the add_volatile class template, adds the volatile qualifier to a type (T). Adding the volatile qualifier if T is already volatile does not change T.

Similar to add_const, if T is a function type, then the compiler will generate a C4180 warning. #pragma warning(disable: 4180) suppresses this warning in Visual Studio.

add_cv

The add_cv template combines add_const and add_volatile.

#pragma warning(push)
#pragma warning(disable: 4180) // Disable C4180: qualifier applied to function type has no meaning; ignored
template<class T>
struct add_cv
{
    using type = const volatile T;
};
#pragma warning(pop)

template<class T>
using add_cv_t = typename add_cv<T>::type;

#pragma warning(push)

#pragma warning(disable: 4180) // Disable C4180: qualifier applied to function type has no meaning; ignored

template<class T>

struct add_cv

{

using type = const volatile T;

};

#pragma warning(pop)

template<class T>

using add_cv_t = typename add_cv<T>::type;

Similar to add_const and add_volatile, we also need to suppress the C4180 compiler warning if we try to use add_cv with a function type.

add_lvalue_reference

The add_lvalue_reference class template is used to create an lvalue reference from a type. We have to be careful since trying to add a reference to non-referenceable type (for example, void is a non-referenceable type) will generate a compilation error. To account for this, we’ll use a helper template that is specialized for referenceable types. Trying to use add_lvalue_reference with a non-referenceable type should produce the original type.

template<class T, class = void>
struct add_lvalue_reference_helper
{
    using type = T;
};

template<class T>
struct add_lvalue_reference_helper<T, void_t<T&>>
{
    using type = T&;
};

template<class T>
struct add_lvalue_reference : add_lvalue_reference_helper<T>
{};

template<class T>
using add_lvalue_reference_t = typename add_lvalue_reference<T>::type;

template<class T, class = void>

struct add_lvalue_reference_helper

{

using type = T;

};

template<class T>

struct add_lvalue_reference_helper<T, void_t<T&>>

{

using type = T&;

};

template<class T>

struct add_lvalue_reference : add_lvalue_reference_helper<T>

{};

template<class T>

using add_lvalue_reference_t = typename add_lvalue_reference<T>::type;

The add_lvalue_reference_helper class template uses SFINAE to safely convert T to T&. If T is a referenceable type, then the partial specialization (lines 7-11) succeeds and add_lvalue_reference_helper<T>::type evaluates to T&. If the partial specialization fails, then T is a non-referenceable type, and the primary template is chosen. In this case, add_lvalue_reference_helper<T>::type evaluates to T.

On lines 13-15, the add_lvalue_reference class template is defined which is derived from add_lvalue_reference_helper allowing the add_lvalue_reference to be defined with a single template parameter. Theoretically, the add_lvalue_reference class template could be implemented without add_lvalue_reference_helper, but then we’d need to define add_lvalue_reference using two template parameters. Since the second template parameter is only used for SFINAE, using add_lvalue_reference_helper allows us to define the add_lvalue_reference class template using a single template parameter.

add_rvalue_reference

Similar to add_lvalue_reference, the add_rvalue_reference class template is used to create an rvalue reference from a type. Once again, we’ll use a helper class template to account for non-referenceable types (such as void).

template<class T, class = void>
struct add_rvalue_reference_helper
{
    using type = T;
};

template<class T>
struct add_rvalue_reference_helper<T, void_t<T&&>>
{
    using type = T&&;
};

template<class T>
struct add_rvalue_reference : add_rvalue_reference_helper<T>
{};

template<class T>
using add_rvalue_reference_t = typename add_rvalue_reference<T>::type;

template<class T, class = void>

struct add_rvalue_reference_helper

{

using type = T;

};

template<class T>

struct add_rvalue_reference_helper<T, void_t<T&&>>

{

using type = T&&;

};

template<class T>

struct add_rvalue_reference : add_rvalue_reference_helper<T>

{};

template<class T>

using add_rvalue_reference_t = typename add_rvalue_reference<T>::type;

The derivation for the add_rvalue_reference class template is similar to that of add_lvalue_reference, so I won’t repeat it here.

Due to reference collapsing rules, add_rvalue_reference<T&> will result in T& not T&&. There are two reference collapsing rules:

An rvalue reference to an rvalue reference becomes becomes an rvalue reference.
All other references to references (all combinations involving an lvalue reference) becomes an lvalue reference.

In the case where T is an lvalue reference, then add_rvalue_reference<T&> will collapse into a lvalue reference^[8].

add_pointer

Similar to add_lvalue_reference and add_rvalue_reference class templates, the add_pointer class template adds a pointer to a give type T. If T is a reference type, then add_pointer<T>::type becomes remove_reference_t<T>*, that is, a pointer is added to the type T, after removing the reference.

Although it is possible to have a reference to a pointer (T*&), it is not possible to add a pointer to a reference (T&*). Attempting to create a pointer to a reference type will result in a compiler error.

template<class T>
auto add_pointer_helper(int) -> type_identity<remove_reference_t<T>*>;

template<class T>
auto add_pointer_helper(...) -> type_identity<T>;

template<class T>
struct add_pointer : decltype(add_pointer_helper<T>(0))
{};

template<class T>
using add_pointer_t = typename add_pointer<T>::type;

template<class T>

auto add_pointer_helper(int) -> type_identity<remove_reference_t<T>*>;

template<class T>

auto add_pointer_helper(...) -> type_identity<T>;

template<class T>

struct add_pointer : decltype(add_pointer_helper<T>(0))

{};

template<class T>

using add_pointer_t = typename add_pointer<T>::type;

Although it is possible to implement the add_pointer class template using a similar technique that is used to implement the add_lvalue_reference and add_rvalue_reference class templates, I want to demonstrate a different technique that utilizes SFINAE to achieve a similar result. Instead of using a struct with partial specialization, we declare two functions.

The first function declared on lines 1-2 takes an int parameter and returns the template argument T with the reference removed and a pointer added to the type wrapped in the type_identity template (which provides the type member).

If T a const, volatile, or reference-qualified function type, then trying to add a pointer to T (T*) would normally generate a compiler error. Instead of generating an error, the compiler will consider the second overload of add_pointer_helper instead.

The second function declared on lines 4-5 is a fallback function that takes any other parameter type using the ellipsis (...) and since the compiler considers this the worst possible match, it only chooses this overload if the compiler fails to instantiate the first version of the function. In this case, the template argument T is wrapped in the identity_type unmodified.

This technique that forces the compiler to choose worse match during function overload resolution is discussed in more detail later in the article (see SFINAE Out Function Overloads)

Both functions can’t take the same parameters (in this case int) because then the function signatures would become ambiguous and would fail to compile. Using the ellipsis (...) tells the compiler to only match this version of the function if it fails to instantiate the first version of the function.

You’ll notice that we provide a declaration of the add_pointer_helper functions but do not provide a definition. This is perfectly fine, as long as these functions are only used in a non-deduced context such as an expression that is only evaluated using the decltype specifier.

On lines 7-9, the add_pointer class template is defined and is derived from the return value of the add_pointer_helper function.

And, as usual, the short-hand alias of the add_pointer class template is defined on lines 11-12.

conditional

In some cases, it is useful to choose a specific type based on some condition. The conditional class template can be used to return one type or another type based on some condition (usually based on another type trait). The conditional class template is equivalent to an if condition in regular C++.

template<bool B, class T, class F>
struct conditional
{
    using type = T;
};

template<class T, class F>
struct conditional<false, T, F>
{
    using type = F;
};

// Helper template alias.
template<bool B, class T, class F>
using conditional_t = typename conditional<B, T, F>::type;

template<bool B, class T, class F>

struct conditional

{

using type = T;

};

template<class T, class F>

struct conditional<false, T, F>

{

using type = F;

};

// Helper template alias.

template<bool B, class T, class F>

using conditional_t = typename conditional<B, T, F>::type;

On lines 1-5 the primary template is defined. When B is true, then the type is an alias of T (let’s call this the true type). However, when the partial specialization where B is false is matched, then type is F (the false type).

Pretty simple right? Let’s see how we can use the conditional class template to implement more complex logical template types.

conjunction

A logical conjunction is a truth-functional operator that is true if and only if all of its operands are true. This is equivalent to a logical AND (&&) operation.

The conjunction class template works by passing any number of type traits that are derived from either true_type or false_type (or has a static member variable value that is convertible to bool) as template arguments to conjunction. The conjunction class template is derived from the first template argument whose value member variable is (or is convertible to) false. If all type traits passed to conjunction are true, then conjunction is derived from the last type trait in the template argument list.

We haven’t looked at many type trait templates that are derived from true_type or false_type yet, but these are introduced later in the article. For now, we just have to keep in mind that a class template that derives from either true_type or false_type has a static const member variable value that is true if it is derived from true_type or false if it is derived from false_type.

We’ll use a recursive variadic template to implement the conjunction class template. First, let’s take a look at the primary template.

// Primary template
template<class...>
struct conjunction : true_type
{};

// Primary template

template<class...>

struct conjunction : true_type

{};

The primary template is a class template that doesn’t specialize any of the template parameters. The compiler will choose this version of the conjunction class template only if there isn’t a specialization of the class template that is a better match. As we’ll see in a second, the primary template will only be chosen when conjunction is used without any template arguments (which is probably a mistake by the programmer). Although the primary template should never be chosen by the compiler, we need it before we can specialize it.

Now let’s take a look at the base case of the recursive variadic template, that is, when conjunction has only a single template argument.

// Specialized for a single template argument.
template<class T>
struct conjunction<T> : T
{};

// Specialized for a single template argument.

template<class T>

struct conjunction<T> : T

{};

In the base case, when conjunction has only a single template argument (T), then conjunction is derived from T. Since all of the template arguments passed to conjunction must have a static member variable called value that is convertible to bool (like true_type and false_type), then conjunction::value is true when T::value is true and false when T::value is false.

Now let’s look at the recursive case:

// Specialized for 2 or more template arguments.
template<class T, class... Tn>
struct conjunction<T, Tn...> : conditional_t<bool(T::value), conjunction<Tn...>, T>
{};

// Specialized for 2 or more template arguments.

template<class T, class... Tn>

struct conjunction<T, Tn...> : conditional_t<bool(T::value), conjunction<Tn...>, T>

{};

The recursive case is used when conjunction has two or more template arguments. In this case, the conditional class template is used to conditionally select either conjunction<Tn...> (recursively calling itself) if T::value is true or T when T::value is false.

Consequently, if T::value is false then the expansion of Tn... stops and no further types need to be instantiated to determine the type of conjunction. This is in contrast to using fold expressions (... && Tn::value) where every T in Tn is instantiated before the expression is evaluated.

In order to reduce some typing later, we’ll also define an inline variable template for conjunction::value:

// Requires C++17
template<class... T>
inline constexpr bool conjunction_v = conjunction<T...>::value;

// Requires C++17

template<class... T>

inline constexpr bool conjunction_v = conjunction<T...>::value;

Now, instead of typing conjunction<...>::value, we only need to type conjunction_v<...>. Small victory, but every little bit helps.

Variable templates require a C++14 compatible compiler. Inline variables requires a C++17 compiler. The inline specifier can be dropped if you need to support C++14.

In my own projects, I use the following macro to support both C++14 and C++17 when available:

#if defined(__cpp_inline_variables) && __cpp_inline_variables >= 201606L
  #define INLINE_VAR inline constexpr
#else
  #define INLINE_VAR constexpr
#endif

#if defined(__cpp_inline_variables) && __cpp_inline_variables >= 201606L

#define INLINE_VAR inline constexpr

#else

#define INLINE_VAR constexpr

#endif

Then prepend inline variable templates with the INLINE_VAR macro instead of inline constexpr.

disjunction

Similar to conjunction, the disjunction class template is equivalent to a logical OR operator.

The disjunction class template works by passing any number of type traits that are derived from either true_type or false_type (or has a static member variable value that is convertible to bool) as template arguments. The disjunction class template is derived from the first template argument whose value member variable is (or is convertible) to true. If all template arguments passed to disjunction are false, then disjunction is derived from the last type trait in the template argument list.

Similar to the implementation of the conjunction class template, we’ll use a recursive variadic template to implement the disjunction class template. First, let’s take a look at the primary template.

// Primary template
template<class...>
struct disjunction : false_type
{};

// Primary template

template<class...>

struct disjunction : false_type

{};

The primary template doesn’t specialize any of the template parameters. The compiler will use the primary template only if there isn’t a specialization of the disjunction class template that is a better match. Since there is a specialization for a single template argument and a specialization for two or more template arguments (see below), the primary template is only chosen when disjunction is used without any template arguments (which is probably a mistake). Although the primary template should never be chosen by the compiler, we need to define it before we can specialize it.

The base case for the recursive variadic template has only a single template parameter:

// Base case
template<class T>
struct disjunction<T> : T
{};

// Base case

template<class T>

struct disjunction<T> : T

{};

In the base case, when the disjunction class template has only a single template argument (T), then disjunction is derived from T. Since all of the template arguments passed to disjunction must have a static member variable called value that is convertible to bool, then disjunction::value is true when T::value is true and false if T::value is false.

Now, let’s look at the recursive case.

template<class T, class... Tn>
struct disjunction<T, Tn...> : conditional_t<bool(T::value), T, disjunction<Tn...>>
{};

template<class T, class... Tn>

struct disjunction<T, Tn...> : conditional_t<bool(T::value), T, disjunction<Tn...>>

{};

The recursive case is instantiated when disjunction is used with two or more template arguments. In this case, the conditional class template is used to conditionally select either T if T::value is true or disjunction<Tn...> (recursively calling itself) if T::value is false.

Consequently, if T::value is true, then the expansion of Tn... stops and no further types need to be instantiated to determine the type of disjunction. This is in contrast to using the fold expression (... || Tn::value) which must instantiate every T in Tn before the expression is evaluated.

And similar to conjunction, we’ll define an inline variable template to create a short-hand for disjunction::value

// Requires C++17
template<class... T>
inline constexpr bool disjunction_v = disjunction<T...>::value;

// Requires C++17

template<class... T>

inline constexpr bool disjunction_v = disjunction<T...>::value;

Now, instead of typing disjunction<...>::value, we only need to type disjunction_v<...>.

negation

The negation class template forms a logical negation of the type trait T.

template<class T>
struct negation : bool_constant<!bool(T::value)>
{};

template<class T>

struct negation : bool_constant<!bool(T::value)>

{};

The negation class template is derived from the bool_constant class template. If T::value is true, then negation::value is false (which is equivalent to being derived from false_type) and if T::value is false, then negation::value is true (which is equivalent to being derived from true_type).

And a short-hand version of negation::value:

// Requires C++17
template<class T>
inline constexpr bool negation_v = negation<T>::value;

// Requires C++17

template<class T>

inline constexpr bool negation_v = negation<T>::value;

With the definition of conditional, conjunction, disjunction, and negation, we have the logical operators that are needed to make any logical combination of type traits that we need. In the following sections, we’ll use these logical class templates as the basis for other type traits.

is_same

The is_same class template is the first class in our type traits library that can actually be considered a type trait. Most type traits result in a boolean value that is either true or false. This is accomplished by inheriting from either true_type if the type trait is true or false_type if the type trait is false.

In most cases, the primary template for the type trait is derived from false_type and one or more partial specializations exist that are derived from true_type.

First, let’s look at the primary template for the is_same type trait.

// Primary template.
template<class T, class U>
struct is_same : false_type
{};

// Primary template.

template<class T, class U>

struct is_same : false_type

{};

The primary template is chosen by the compiler when T and U are different types. Next, we’ll create a partial specialization of is_same when T and U are the same types.

// Specialization for matching types.
template<class T>
struct is_same<T, T> : true_type
{};

// Specialization for matching types.

template<class T>

struct is_same<T, T> : true_type

{};

The partial specialization is only chosen when T and U are exactly the same types. That means that their const, volatile, reference or pointer attributes must also be the same. If you want to ignore any const, volatile, or references that might adorn the type, then wrap the type in either the remove_cv or remove_cvref class template.

A short-hand for is_same::value can be defined using a variable template (requires C++14):

// Requires C++17
template<class T, class U>
inline constexpr bool is_same_v = is_same<T, U>::value;

// Requires C++17

template<class T, class U>

inline constexpr bool is_same_v = is_same<T, U>::value;

is_void

With the is_same and remove_cv type traits defined, we can use these to define other type traits which can be used to identify all of the primary types. The is_void type trait evaluates to true_type if the template argument is void (ignoring any const and volatile qualifiers) and false_type otherwise.

template<class T>
struct is_void : is_same<void, remove_cv_t<T>>
{};

template<class T>

struct is_void : is_same<void, remove_cv_t<T>>

{};

As was shown in the previous section, the is_same type trait is derived from true_type when the first and second template arguments are exactly the same type, and false_type otherwise. We can use this to define a type trait that checks for a primary type (like ints and floats which we’ll look at in the following sections).

We’ll also define an inline variable template called is_void_v that can be used as a short-hand for is_void::value:

// Requires C++17
template<class T>
inline constexpr bool is_void_v = is_void<T>::value;

// Requires C++17

template<class T>

inline constexpr bool is_void_v = is_void<T>::value;

is_null_pointer

Similar to the is_void type trait, the is_null_pointer type trait is derived from true_type if the template argument is std::nullptr_t.

#include <cstddef> // for std::nullptr_t

template<class T>
struct is_null_pointer : is_same<std::nullptr_t, remove_cv_t<T>>
{};

// Requires C++17
template<class T>
inline constexpr bool is_null_pointer_v = is_null_pointer<T>::value;

#include <cstddef> // for std::nullptr_t

template<class T>

struct is_null_pointer : is_same<std::nullptr_t, remove_cv_t<T>>

{};

// Requires C++17

template<class T>

inline constexpr bool is_null_pointer_v = is_null_pointer<T>::value;

The implementation of is_null_pointer is similar to is_void.

is_any_of

The is_any_of type trait can be used to check if a certain type template argument matches any one of the other type template arguments. We’ll use the disjunction and the is_same type traits defined earlier to implement the is_any_of type trait.

The is_any_of type trait does not currently exist in the C++ standard, but we’ll use this type trait to simplify the defintion of other type traits later in this article.

template<class T, class... Tn>
struct is_any_of : disjunction<is_same<T, Tn>...>
{};

// Requires C++17
template<class T, class... Tn>
inline constexpr bool is_any_of_v = is_any_of<T, Tn...>::value;

template<class T, class... Tn>

struct is_any_of : disjunction<is_same<T, Tn>...>

{};

// Requires C++17

template<class T, class... Tn>

inline constexpr bool is_any_of_v = is_any_of<T, Tn...>::value;

The implementation of the is_any_of type trait is super simple since we can rely on the disjunction and the is_same type traits that were previously defined. Variadic template arguments are used to check if the type T matches any one of types in the pack represented by Tn.

is_integral

With the is_any_of type trait defined previously, it is now super simple to implement other type traits. The is_integral type trait is true_type if the template argument is one of the following types:

bool
char
char8_t (since C++20)
char16_t
char32_t
wchar_t
short
int
long
long long

Or any other equivalent type including signed or unsigned, with const, and volatile qualified variants. Otherwise, it is false_type.

template<class T>
struct is_integral : is_any_of<remove_cv_t<T>,
    bool,
    char,
    signed char,
    unsigned char,
    wchar_t,
    char16_t,
    char32_t,
    short,
    unsigned short,
    int,
    unsigned int,
    long,
    unsigned long,
    long long,
    unsigned long long
#if defined(__cpp_char8_t) && __cpp_char8_t >= 201811L
    , char8_t // Since C++20
#endif
>
{};

// Requires C++17
template<class T>
inline constexpr bool is_integral_v = is_integral<T>::value;

template<class T>

struct is_integral : is_any_of<remove_cv_t<T>,

bool,

char,

signed char,

unsigned char,

wchar_t,

char16_t,

char32_t,

short,

unsigned short,

int,

unsigned int,

long,

unsigned long,

long long,

unsigned long long

#if defined(__cpp_char8_t) && __cpp_char8_t >= 201811L

, char8_t // Since C++20

#endif

{};

// Requires C++17

template<class T>

inline constexpr bool is_integral_v = is_integral<T>::value;

Using the is_any_of type trait defined previously, the is_intgral type trait becomes much simpiler. If the template argument T is any one of the types listed (after removing const and volatile qualifiers), then is_integral is true_type, otherwise it is false_type.

is_floating_point

Similar to the is_integral type trait, the is_floating_point type trait is true_type if the template argument is one of the following types:

Including const and volatile qualified variants. Otherwise, it is false_type.

template<class T>
struct is_floating_point : is_any_of<remove_cv_t<T>,
    float,
    double,
    long double
>
{};

// Requires C++17
template<class T>
inline constexpr bool is_floating_point_v = is_floating_point<T>::value;

template<class T>

struct is_floating_point : is_any_of<remove_cv_t<T>,

float,

double,

long double

{};

// Requires C++17

template<class T>

inline constexpr bool is_floating_point_v = is_floating_point<T>::value;

is_arithmetic

The is_arithmetic type trait is true_type if its template argument is either an integral type or a floating-point type, and false_type otherwise. As you may have guessed, we can use the is_integral and is_floating_point type traits defined earlier in combination with disjunction to implement this type trait.

template<class T>
struct is_arithmetic : disjunction<is_integral<T>, is_floating_point<T>>
{};

// Requires C++17
template<class T>
inline constexpr bool is_arithmetic_v = is_arithmetic<T>::value;

template<class T>

struct is_arithmetic : disjunction<is_integral<T>, is_floating_point<T>>

{};

// Requires C++17

template<class T>

inline constexpr bool is_arithmetic_v = is_arithmetic<T>::value;

An an alternative and equivalent implementation of the is_arithmetic type trait uses the bool_constant class template directly:

template<class T>
struct is_arithmetic : bool_constant<is_integral_v<T> || is_floating_point_v<T>>
{};

template<class T>

struct is_arithmetic : bool_constant<is_integral_v<T> || is_floating_point_v<T>>

{};

Although it doesn’t change the meaning of the is_arithmetic type trait, it demonstrates that you can use the logical OR operator (||) to evaluate template arguments. Note however that the disjunction class template expects its template arguments to be types, while the bool_constant class template expects a non-type template argument that is convertible to bool. In this case, we can use the _v short-hand variants of the type traits to get the value member variable of the type trait.

is_const

The is_const type trait checks to see if a type is const-qualified. The is_const type trait is derived from true_type if the type is const-qualified, or false_type otherwise.

template<class T>
struct is_const : false_type
{};

template<class T>
struct is_const<const T> : true_type
{};

// Required C++17
template<class T>
inline constexpr bool is_const_v = is_const<T>::value;

template<class T>

struct is_const : false_type

{};

template<class T>

struct is_const<const T> : true_type

{};

// Required C++17

template<class T>

inline constexpr bool is_const_v = is_const<T>::value;

Similar to the remove_const class template that was previously shown, the is_const type trait uses partial specialization to detect const-qualified types.

is_reference

The is_reference type trait can be used to check if a type is either an lvalue reference or rvalue reference type.

template<class T>
struct is_reference : false_type
{};

template<class T>
struct is_reference<T&> : true_type
{};

template<class T>
struct is_reference<T&&> : true_type
{};

template<class T>

struct is_reference : false_type

{};

template<class T>

struct is_reference<T&> : true_type

{};

template<class T>

struct is_reference<T&&> : true_type

{};

The is_reference type trait is derived from true_type if the type T is either an lvalue (line 6) or an rvalue (line 10) reference. Otherwise, is_reference is derived from false_type.

And the short-hand version:

template<class T>
inline constexpr bool is_reference_v = is_reference<T>::value;

1 2	template<class T> inline constexpr bool is_reference_v = is_reference<T>::value;

is_bounded_array

The is_bounded_array type trait checks if T is an array type with a known size.

template<class T>
struct is_bounded_array : false_type
{};

template<class T, std::size_t N>
struct is_bounded_array<T[N]> : true_type
{};

template<class T>

struct is_bounded_array : false_type

{};

template<class T, std::size_t N>

struct is_bounded_array<T[N]> : true_type

{};

If T is a bounded array (an array with a known size in the form of T[N]), then is_bounded_array is derived from true_type, otherwise it is derived from false_type.

And the short-hand variant:

// Requires C++17
template<class T>
inline constexpr bool is_bounded_array_v = is_bounded_array<T>::value;

// Requires C++17

template<class T>

inline constexpr bool is_bounded_array_v = is_bounded_array<T>::value;

is_unbounded_array

The type trait for an unbounded array is very similar to that of the bounded array. The primary difference is that the size of the array is unspecified.

template<class T>
struct is_unbounded_array : false_type
{};

template<class T>
struct is_unbounded_array<T[]> : true_type
{};

// Requires C++17
template<class T>
inline constexpr bool is_unbounded_array_v = is_unbounded_array<T>::value;

template<class T>

struct is_unbounded_array : false_type

{};

template<class T>

struct is_unbounded_array<T[]> : true_type

{};

// Requires C++17

template<class T>

inline constexpr bool is_unbounded_array_v = is_unbounded_array<T>::value;

is_array

The is_array type trait can be used to check if a type is either a bounded or unbounded array.

template<class T>
struct is_array : bool_constant<is_bounded_array_v<T> || is_unbounded_array_v<T>>
{};

// Requires C++17
template<class T>
inline constexpr bool is_array_v = is_array<T>::value;

template<class T>

struct is_array : bool_constant<is_bounded_array_v<T> || is_unbounded_array_v<T>>

{};

// Requires C++17

template<class T>

inline constexpr bool is_array_v = is_array<T>::value;

is_function

The is_function type trait can be used to check if a type is a function. The is_function type trait only considers free functions and static member functions of a class to be function types. std::function, lambdas, callable function objects (classes or structs with overloaded function call operator operator()) and pointers to functions are not considered function types.

#pragma warning(push)
#pragma warning(disable: 4180) // Disable C4180: qualifier applied to function type has no meaning; ignored
template<class T>
struct is_function : bool_constant<!is_const_v<const T> && !is_reference_v<T>>
{};
#pragma warning(pop)

template<class T>
inline constexpr bool is_function_v = is_function<T>::value;

#pragma warning(push)

#pragma warning(disable: 4180) // Disable C4180: qualifier applied to function type has no meaning; ignored

template<class T>

struct is_function : bool_constant<!is_const_v<const T> && !is_reference_v<T>>

{};

#pragma warning(pop)

template<class T>

inline constexpr bool is_function_v = is_function<T>::value;

The is_function type trait works on the basis that only function types and reference types can’t be const-qualified. Adding the const qualifier to a function type does not change its constness. If T is a function type (or a reference type), then is_const_v<const T> will be false. If is_reference_v<T> is also false, then T must be a function type.

In fact, trying to add a const qualifier to a function type will generate a warning (C4180) in Visual Studio. The warning about applying a const qualifier to a function type can be disabled using the #pragma warning(disable: 4180) pragma as shown in the code snippet.

decay

The decay class template is used to perform the same conversion operations that are applied to template arguments when passed by value. The decay class template will do one of three things depending on the argument type:

Array: If T is an array of type U (either an unbounded array of the form U[] or a bounded array of the form U[N]) then decay<T>::type will be U*. That is, array types decay to pointers to the array element type.
Function: If T is a function type or a reference to a function, then decay<T>::type will be add_pointer_t<T>. That is, function types become pointers to functions.
Neither array nor function: decay<T>::type removes any reference, const, and volatile qualifiers from the type using remove_cv_t<remove_reference_t<T>>

We’ll use a piecewise technique to implement the decay class template that is split into 3 parts:

The primary template which is used when T is neither an array type nor a function type.
A partial specialization when T is an array type.
A partial specialization when T is a function type.

Similar to how we implemented add_lvalue_reference, and add_rvalue_reference, we’ll use a helper class template so that the decay class template only requires a single template parameter.

First, we’ll look at the primary template for the decay_helper class template.

template<class T, 
    bool IsArray = is_array_v<T>, 
    bool IsFunc = is_function_v<T>
>
struct decay_helper
{
    using type = remove_cv_t<T>;
};

template<class T,

bool IsArray = is_array_v<T>,

bool IsFunc = is_function_v<T>

struct decay_helper

{

using type = remove_cv_t<T>;

};

The primary template for the decay_helper class template takes three template arguments:

T: The type to decay,
IsArray: A boolean non-type template parameter that is true if T is an array type or false otherwise.
IsFunc: A boolean non-type template parameter that is true if T is a function type or false otherwise.

The IsArray template parameter defaults to is_array_v<T> and the IsFunc template parameter defaults to is_function_v<T>.

Since we will provide a partial specialization when T is an array type and another specialization for when T is a function type, the primary template is only used when T is neither an array nor a function type (that is, both IsArray and IsFunc are false).

When T is neither an array nor a function type, we’ll use the remove_cv class template to remove any const, and volatile qualifiers from T.

Next, we’ll provide a partial specialization of decay_helper when T is an array type.

template<class T>
struct decay_helper<T, true, false>
{
    using type = remove_extent_t<T>*;
};

template<class T>

struct decay_helper<T, true, false>

{

using type = remove_extent_t<T>*;

};

This partial specialization will be used when is_array_v<T> evaluates to true and is_function_v<T> evaluates to false. In this case, the resulting type is remove_extent_t<T>*, which removes the array extent from the type and adds a pointer to the resulting element type.

Next, we’ll provide a partial specialization of decay_helper when T is a function type.

template<class T>
struct decay_helper<T, false, true>
{
    using type = add_pointer_t<T>;
};

template<class T>

struct decay_helper<T, false, true>

{

using type = add_pointer_t<T>;

};

This partial specialization is used when is_array_v<T> evaluates to false and is_function_v<T> evaluates to true. In this case, we just add a pointer to the function type using the add_pointer class template.

With all the possible combinations handled, we can now define the decay class template.

template<class T>
struct decay
{
    using type = typename decay_helper<remove_reference_t<T>>::type;
};

template<class T>
using decay_t = typename decay<T>::type;

template<class T>

struct decay

{

using type = typename decay_helper<remove_reference_t<T>>::type;

};

template<class T>

using decay_t = typename decay<T>::type;

The decay class template uses the decay_helper class template to determine the type of the type member after removing any references from T.

And of course, on lines 28-29, the short-hand alias template for typename decay<T>::type is defined.

SFINAE

SFINAE (sfee-nay) is an acronym for “Substitution Failure Is Not An Error” and it refers to a technique used by the compiler to turn potential errors into “deduction failures” during template argument deduction. It is a technique used to eliminate certain functions from being chosen during overload resolution or to choose a particular class template specialization based on characteristics of the template arguments. If the compiler finds an invalid expression during template argument deduction, instead of generating a compiler error, it removes that function or class specialization from the set of possible candidates.

We’ve already seen a few examples of using SFINAE to generate a few of the type traits in the previous sections. The add_pointer type trait uses a set of function overloads to SFINAE-out the case where adding a pointer to T would result in an error. For example, if T was a const, volatile or reference qualified function type, then attempting to add a pointer to T would generate a compile-time error. Instead of generating an error, the compiler eliminates the first function from the set of overloads and considers the next function.

Another SFINAE technique is used to define the add_lvalue_reference and add_rvalue_reference type traits. Instead of function overloads, partial specialization of a class template is used to SFINAE-out cases where adding a reference to T would result in a compiler error (for example, if T is void).

SFINAE-Out Function Overloads

To demonstrate SFINAE using function template overloads, we’ll create a SFINAE-based type trait to determine if a type T is constructible using a particular set of arguments (Args...).

The approach to implementing SFINAE-based traits with function overloads is to declare two overloaded function templates named test (you can use any name for this function, but test is traditionally used for SFINAE-based traits).

template<...>
true_type test(int);

// fallback
template<...>
false_type test(...);

template<...>

true_type test(int);

// fallback

template<...>

false_type test(...);

The first overload version of the test function template takes an int (any parameter type can be used, but int seems like a good choice) and returns true_type. This version of the function template is used if the template parameters for the provided template arguments are well-formed.

The second overload of the test function is called the fallback and takes any argument types using the ellipsis operator (...). Since the compiler considers functions taking the ellipsis operator the worst possible match during function overload resolution, the second version of the test function will only be chosen if the template parameters in the first overload are not well formed. In this case, the fallback for the test function returns false_type.

The form of the template parameters for the overload that returns true_type should only be valid if (and only if) the condition we want to check is true. In this case, we want to check if it is possible to construct a type T from a given set of arguments (Args...). That is, we want to check if T(Args...) is valid.

To avoid name clashes in the current scope, the test functions are wrapped in a struct called is_constructible_helper.

struct is_constructible_helper
{
    template<class T, class... Args, class = decltype(::new T(std::declval<Args>()...))>
    static true_type test(int);

    template<class...>
    static false_type test(...);
};

struct is_constructible_helper

{

template<class T, class... Args, class = decltype(::new T(std::declval<Args>()...))>

static true_type test(int);

template<class...>

static false_type test(...);

};

The is_constructible_helper declares (but does not define) two static member function templates called test. The first version of the test function template takes a type T (the type we are testing) and a variadic set of arguments Args... (the arguments we are using to test if it is possible construct an instance of T). If the expression ::new T(Args...) is valid, then the first version of the test function is chosen during overload resolution.

See decltype and std::declval if you’re not sure what they do.

If, for any reason, the expression ::new T(Args...) is not a valid expression, then the compiler will choose the second overload of the test function, which returns false_type.

Next, we’ll define the is_constructible trait that is derived from true_type if T(Args...) is valid, or false_type otherwise.

template <class T, class... Args>
struct is_constructible : decltype(is_constructible_helper::test<T, Args...>(0))
{};

template <class T, class... Args>

struct is_constructible : decltype(is_constructible_helper::test<T, Args...>(0))

{};

The is_constructible class template is derived from the return type of one of the test functions. As was just derived, this will be either true_type if T can be constructed from Args..., or false_type otherwise.

Next, we’ll implement the exact same SFINAE-based type trait, but this time using partial specialization of a class template.

SFINAE-Out Partial Specializations

Using function overloads is one technique to implement SFINAE-based traits. Another technique uses partial specialization of a class template. Let’s see how we can implement the is_constructible type trait using partial specialization.

The basic principal for using partial specialization for implementing SFINAE-based type traits is to first define the primary template (the template that does not specialize any of the template parameters) which is derived from false_type and define a partial specialization that is derived from true_type that tests the condition we want to check for. Since the compiler consider a partial specialization a better match than the primary template, the partial partial specialization is used when the template arguments are well-formed.

template<class, class T, class... Args>
struct is_constructible_helper : false_type
{};

template<class T, class... Args>
struct is_constructible_helper<void_t<decltype(::new T(std::declval<Args>()...))>,
    T, Args...> : true_type
{};

template<class, class T, class... Args>

struct is_constructible_helper : false_type

{};

template<class T, class... Args>

struct is_constructible_helper<void_t<decltype(::new T(std::declval<Args>()...))>,

T, Args...> : true_type

{};

The primary template is defined on lines 1-3. The primary template has three template parameters. The first (unnamed) template parameter is a dummy placeholder for the condition we want to check. The 2nd and 3rd template parameters are the T and Args... that we want to check if T is constructible from Args....

In most cases, the dummy placeholder template parameter that is used to check the condition appears as the last template parameter in the parameter list. However in this case, the type trait uses a template parameter pack, which must appear at the end of the template parameter list.

The specialized version on lines 5-8 uses void_t to test if the expression is valid. As was described earlier in the post, void_t can be used with SFINAE-based expressions when the resulting type is not used (since void_t maps any number of template arguments to void). In this case, we don’t care about the type that results from the expression, we just want to test if the expression is valid.

With the helper template defined, we can then create the actual type trait that is derived from the helper trait.

template<class T, class... Args>
struct is_constructible : is_constructible_helper<void, T, Args...>
{};

template<class T, class... Args>

struct is_constructible : is_constructible_helper<void, T, Args...>

{};

Whether we use function overloads or partial specialization to define the SFINAE-based type traits, we can define the short-hand version of the type trait the same way:

// Requires C++17.
template<class T, class... Args>
inline constexpr bool is_constructible_v = is_constructible<T, Args...>::value;

// Requires C++17.

template<class T, class... Args>

inline constexpr bool is_constructible_v = is_constructible<T, Args...>::value;

SFINAE with enable_if

The enable_if trait uses SFINAE to disable certain function overloads from being considered during overload resolution. As is described earlier, the enable_if trait defines a member called type (which defaults to void) only if the first template argument to enable_if evaluates to true. If the first template argument to enable_if is false, then type is not defined and attempting to use it would result in a substitution failure.

The enable_if utility can be used as:

An additional (type or non-type) template parameter,
An additional function argument,
The return type of a function

To demonstrate the various ways that enable_if utility can be used to SFINAE-out function overloads, suppose we have a struct called Scalar that can hold either an int, a float, or a double, but no other types are allowed. We want to be able to retrieve the stored value, and update the stored value. Trying to retrieve the internal value using a different type than the stored type or trying to set the stored value to a type other than the stored type should produce an error (either by throwing an exception or by triggering an assertion. For this simple demo, we will use asserts if there is a type mismatch).

The Scalar class shown here is purely for demonstration purposes only. I do not recommend you implement something like this in your own projects. In practice, std::variant (since C++17) would be a much better choice for solving this kind of problem.

For this example, we also define a few type traits to check for int, float, and double types.

template<typename T>
struct is_int : is_same<remove_cvref_t<T>, int>
{};

template<typename T>
inline constexpr bool is_int_v = is_int<T>::value;

template<typename T>
struct is_float : is_same<remove_cvref_t<T>, float>
{};

template<typename T>
inline constexpr bool is_float_v = is_float<T>::value;

template<typename T>
struct is_double : is_same<remove_cvref_t<T>, double>
{};

template<typename T>
inline constexpr bool is_double_v = is_double<T>::value;

template<typename T>

struct is_int : is_same<remove_cvref_t<T>, int>

{};

template<typename T>

inline constexpr bool is_int_v = is_int<T>::value;

template<typename T>

struct is_float : is_same<remove_cvref_t<T>, float>

{};

template<typename T>

inline constexpr bool is_float_v = is_float<T>::value;

template<typename T>

struct is_double : is_same<remove_cvref_t<T>, double>

{};

template<typename T>

inline constexpr bool is_double_v = is_double<T>::value;

You should be familiar with the construct of the is_int, is_float, and is_double type traits. If you need a refresher, check out remove_cvref, is_same, is_integral, and is_floating_point.

First, we will see how enable_if can be used as an additional template parameter to choose a function overload based on type traits.

As a Template Parameter

For the Scalar class, we will use enable_if utility to SFINAE-out the constructor based on the type that is used to initialize an instance of Scalar.

class Scalar
{
    enum class Type
    {
        Integer,
        Float,
        Double
    };

    const Type m_Type;

    union
    {
        int m_Int;
        float m_Float;
        double m_Double;
    };

public:
    template<typename I, enable_if_t<is_int_v<I>>* = nullptr>
    Scalar(I i)
        : m_Type(Type::Integer)
        , m_Int(i)
    {}

    template<typename F, enable_if_t<is_float_v<F>>* = nullptr>
    Scalar(F f)
        : m_Type(Type::Float)
        , m_Float(f)
    {}

    template<typename D, enable_if_t<is_double_v<D>>* = nullptr>
    Scalar(D d)
        : m_Type(Type::Double)
        , m_Double(d)
    {}

class Scalar

{

enum class Type

{

Integer,

Float,

Double

};

const Type m_Type;

union

{

int m_Int;

float m_Float;

double m_Double;

};

public:

template<typename I, enable_if_t<is_int_v<I>>* = nullptr>

Scalar(I i)

: m_Type(Type::Integer)

, m_Int(i)

{}

template<typename F, enable_if_t<is_float_v<F>>* = nullptr>

Scalar(F f)

: m_Type(Type::Float)

, m_Float(f)

{}

template<typename D, enable_if_t<is_double_v<D>>* = nullptr>

Scalar(D d)

: m_Type(Type::Double)

, m_Double(d)

{}

In this example, three constructors for the Scalar class are defined on lines 41-57. The constructors are template member functions that have two template parameters.

The first template parameter is the type of the passed parameter.
The second template parameter uses enable_if to SFINAE-out the constructor based on the type of the first template parameter.

The construct of the second template parameter might look strange. Let’s take a closer look at the first constructor:

struct Scalar
{
    template<typename I, enable_if_t<is_int_v<I>>* = nullptr>
    Scalar(I i)
    ...

struct Scalar

{

template<typename I, enable_if_t<is_int_v<I>>* = nullptr>

Scalar(I i)

...

The second template parameter doesn’t use typename to declare the template parameter. This is because the second template parameter is a non-type template parameter. If I is an int, then this is what the compiler would produce:

struct Scalar
{
    template<typename I, void* = nullptr>
    Scalar(I i)
    ...

struct Scalar

{

template<typename I, void* = nullptr>

Scalar(I i)

...

Since pointer types are perfectly valid as non-type template parameters (see Non-type Template Parameters), this code compiles.

A common mistake when using enable_if as an additional template parameter, is to use it as a type template parameter with a default template argument like this:

    template<typename I, typename = enable_if_t<is_int_v<I>>>
    Scalar(I i)
	...

template<typename I, typename = enable_if_t<is_int_v<I>>>

Scalar(I i)

...

But this only creates an ambiguous function overload since the default template arguments are not taken into consideration during overload resolution and cannot be used to SFINAE-out function overloads!

Only failures in the types and expressions in the immediate context of a function type or its template parameter types are SFINAE errors. Default template arguments are not part of the immediate context and therefore cannot be used to SFINAE-out function overloads.

Next, we’ll see how enable_if can be used as an additional function argument to SFINAE-out function overloads.

As a Function Argument

enable_if can also be used as an additional function argument. To demonstrate this, we’ll implement a set of functions called set in the Scalar class that are used to update the internal value. The overload that is used is determined by the type of the first function argument to the set function.

    template<typename I>
    void set(I i, enable_if_t<is_int_v<I>>* = nullptr)
    {
        assert(m_Type == Type::Integer);
        m_Int = i;
    }

    template<typename F>
    void set(F f, enable_if_t<is_float_v<F>>* = nullptr)
    {
        assert(m_Type == Type::Float);
        m_Float = f;
    }

    template<typename D>
    void set(D d, enable_if_t<is_double_v<D>>* = nullptr)
    {
        assert(m_Type == Type::Double);
        m_Double = d;
    }

template<typename I>

void set(I i, enable_if_t<is_int_v<I>>* = nullptr)

{

assert(m_Type == Type::Integer);

m_Int = i;

}

template<typename F>

void set(F f, enable_if_t<is_float_v<F>>* = nullptr)

{

assert(m_Type == Type::Float);

m_Float = f;

}

template<typename D>

void set(D d, enable_if_t<is_double_v<D>>* = nullptr)

{

assert(m_Type == Type::Double);

m_Double = d;

}

Similar to the way that enable_if is used to SFINAE-out the constructors, it is used here as an additional function argument to SFINAE-out the overload of the set member function.

In the case of the first overload on lines 59-60, if I is an int, this is what the compiler produces:

    void set(int i, void* = nullptr)
    {
        assert(m_Type == Type::Integer);
        m_Int = i;
    }

void set(int i, void* = nullptr)

{

assert(m_Type == Type::Integer);

m_Int = i;

}

Optionally, we can name the second parameter, but since it’s not being used in the body of the function, doing so may cause a warning about the unused function parameter. Omitting the name of the unused function parameters avoids that warning.

Another way to use enable_if to SFINAE-out function overloads is as the return type of the function.

As a Return Type

enable_if can also be used as the return type of a function. To demonstrate this, we’ll create a set of member functions for the Scalar class called get:

    template<typename I>
    enable_if_t<is_int_v<I>, I> get() const
    {
        assert(m_Type == Type::Integer);
        return m_Int;
    }

    template<typename F>
    enable_if_t<is_float_v<F>, F> get() const
    {
        assert(m_Type == Type::Float);
        return m_Float;
    }

    template<typename D>
    enable_if_t<is_double_v<D>, D> get() const
    {
        assert(m_Type == Type::Double);
        return m_Double;
    }

template<typename I>

enable_if_t<is_int_v<I>, I> get() const

{

assert(m_Type == Type::Integer);

return m_Int;

}

template<typename F>

enable_if_t<is_float_v<F>, F> get() const

{

assert(m_Type == Type::Float);

return m_Float;

}

template<typename D>

enable_if_t<is_double_v<D>, D> get() const

{

assert(m_Type == Type::Double);

return m_Double;

}

If you recall from the derivation of the enable_if utility template, the second template argument is the type that is used for the return value of the function if the first template argument evaluates to true. In this case, we could have written:

    template<typename I>
    enable_if_t<is_int_v<I>, int> get() const
    ...

template<typename I>

enable_if_t<is_int_v<I>, int> get() const

...

Which may have been a better choice since we know I must be int if this overload is chosen. Regardless, the return value of the function is actually the second template argument of the enable_if utility template.

In this case, there are three overloads of the get function. The version of the get function that is chosen during overload resolution is determined by the type of the template argument. For example, if the template argument is int, then the compiler will generate something like this:

    int get() const
    {
        assert(m_Type == Type::Integer);
        return m_Int;
    }

int get() const

{

assert(m_Type == Type::Integer);

return m_Int;

}

We’ve now seen three ways of using enable_if to SFINAE-out function template overloads. But what is the best technique to use? Let’s look at that next.

Summary

To summarize, we’ve seen three different techniques showing how to use enable_if to SFINAE-out function template overloads. The following table attempts to summarize when you should use which technique.

Usage	Use Case
Template Parameter	When used with special member functions like constructors and destructors that don’t have a return type. Also for operator overloads of a class that have a specific function signature with a fixed number of function arguments.
Function Argument	There is probably no good use case for using this form. Since it adds an additional parameter to the function signature, you add the risk that the end user thinks that they need to pass an argument. The dummy argument also appears in IntelliSense in the Visual Studio IDE (or whatever IDE you are using) which may cause more confusion for the poor end user who doesn’t understand the `enable_if` construct. I would advise against using `enable_if` as a function argument.
Return Type	Whenever possible. Using `enable_if` as the return type of a function does not change the number of template parameters nor the number of function arguments, this is arguably the least intrusive way of using `enable_if`. This form should be preferred whenever possible.

If you think that the use of enable_if is clumsy and makes the code harder to read, well then join the club. Luckily the C++ standards committee agrees with you, which is why C++20 introduces concepts.

Concepts

In the previous section, we used enable_if to constrain the types of template parameters in class and function templates. Although it is possible to use enable_if to impose constraints on template parameters, it’s not the the most elegant syntax, nor does it improve the readability of the diagnostic error messages produced by the compiler when those constraints are violated. C++20 concepts are a way to express a set of constraints on template parameters that make it possible to:

Clearly communicate the constraints on template parameters, providing better “self-documenting code”
Improve the diagnostic error messages from a compiler when constraints are not met
Specialize function and class templates based on a set of type constraints

Concept Definition

A concept refers to a template for a named set of constraints where each constraint is defined by one or more requirements for the set of template parameters. A concept definition has the following form:

template< template-parameter-list >
concept concept-name = constraint-expression;

A concept’s parameter list specifies one or more template parameters. Similar to function and class templates, these can be either type or non-type template parameters. Unlike regular templates, concepts are never instantiated by the compiler and they never produce code that is executed at run-time. They are used to define a set of constraints on the template parameters that the compiler uses to check if the type satisfies those constraints.

The constraints in the constraint expression is a logical set of boolean expressions that consists of conjunctions (using &&) and disjunctions (using ||) that must evaluate (at compile time) to either true if the constraints on the template parameter are satisfied, or false otherwise.

If a type T satisfies the constraint expression, that is, the constraint expression evaluates to true for the given type T, then it is said that the type T models the concept.

template <typename T>
concept Small = sizeof(T) <= sizeof(int);

1 2	template <typename T> concept Small = sizeof(T) <= sizeof(int);

In the above example, the type T models the Small concept if the size of T is not larger than the size of an int.

Besides regular C++ expressions, the constraint expression can be defined in terms of type traits (that evaluate to true or false) and they can also be either a concept expression, or a requires expression.

In the following sections, we will look at concept expressions and requires expressions.

Concept Expression

A concept expression is used to verify if a give type models a concept. A concept expression consists of the name of a previously defined concept followed by a set of template arguments between angle brackets. For example, Small<char> and Small<short> are concept expressions that evaluate to true, but Small<double> and Small<long double> generally evaluate to false.

Concepts can be defined in terms of previously defined named concepts by using a concept expression.

template <class T>
concept Integral = is_integral_v<T>;

template <class T>
concept SignedIntegral = Integral<T> && is_signed_v<T>;

template <class T>
concept UnsignedIntegral = Integral<T> && !SignedIntegral<T>;

template <class T>

concept Integral = is_integral_v<T>;

template <class T>

concept SignedIntegral = Integral<T> && is_signed_v<T>;

template <class T>

concept UnsignedIntegral = Integral<T> && !SignedIntegral<T>;

In this example, the SignedIntegral concept is defined in terms of the previously defined Integral concept, and the UnsignedIntegral is in-turn defined by the previously defined Integral and SignedIntegral concepts.

Although you can get pretty far with defining concepts using concept expressions, at some point, you may find that there isn’t a concept expression that tests the requirements of the type that you need. In this case you can use a requires expression.

Requires Expression

A requires expression has one of the following forms:

requires { requirement-seq }
requires ( parameter-list ) { requirement-seq }

The optional parameter list is a comma-separated list of typed arguments that can be used in the requirement sequence. The requirement sequence is a list of one or more expressions that are evaluated by the compiler. The expressions in the requirement sequence never produces executable code. They are only used by the compiler to check if the expressions form valid C++ code.

Each requirement in the requirement sequence can be one of the following types:

Simple requirement
Type requirement
Compound requirement
Nested requirement

In the following sections, we’ll look at each type of requirement.

Simple Requirement

A simple requirement is an arbitrary C++ expression that is evaluated by the compiler for correctness. A simple requirement has one of the the following forms:

requires { simple-requirement; }
requires ( parameter-list ) { simple-requirement; }

An example of a simple requirement that checks if two types can be added together might look like this:

template<class T, class U>
concept Addable = requires (const T& t, const U& u) {
    t + u;
};

template<class T, class U>

concept Addable = requires (const T& t, const U& u) {

t + u;

};

The Addable concept shown here is simplified for demonstration purposes. For example, you may want to check if both t + u and u + t are valid expressions. You may also want to account for cases where T and U are already reference types by adding remove_reference_t to the parameter types.

A simple requirement is just a C++ expression that is terminated by a semicolon (;).

Type Requirement

A type requirement is used to check for the existence of a named nested type. A type requirement has the following form:

requires { typename name; }
requires ( parameter-list ) { typename name; }

Where name refers to a nested member type, an alias type, or a class template type.

The following example checks if the template argument T has a nested member type called value_type:

template<class T>
concept HasValueType = requires {
    typename T::value_type;
};

template<class T>

concept HasValueType = requires {

typename T::value_type;

};

Another common usage for a type requirement is to check if a given type can be used to instantiate a specific class template. For example, if your code requires some template argument to be used with an std::vector, then you can check that with this concept:

#include <vector>

template<class T>
concept WorksWithVectors = requires {
    typename std::vector<T>;
};

#include <vector>

template<class T>

concept WorksWithVectors = requires {

typename std::vector<T>;

};

The WorksWithVectors concept checks if instantiating std::vector<T> would not produce a compiler error.

The WorksWithVectors concept may erroneously succeed with abstract class types. The WorksWithVectors concept only checks if a vector can be instantiated with a specific type, but it does not check any of the operations that can be performed on an std::vector of type T.

Compound Requirement

Similar to simple requirements, compound requirements are used to check the validity of a C++ expression. In addition to simple requirements, compound requirements can also verify that the result of the expression meets some kind of type constraint or that the expression does not throw an exception.

Compound requirements have one of the following forms:

requires { { compound-requirement }; }                             // Same as a simple requirement
requires { { compound-requirement } noexcept; }                    // compound-requirement does not throw an exception
requires { { compound-requirement } -> type-constraint; }          // The result of compound-requirement satisfies type-constraint
requires { { compound-requirement } noexcept -> type-constraint; } // The result of compound-requirement satisfies type-constraint and does not throw an exception
// And parameter-list variants:
requires ( parameter-list ) { { compound-requirement }; }                             // Same as a simple requirement
requires ( parameter-list ) { { compound-requirement } noexcept; }                    // compound-requirement does not throw an exception
requires ( parameter-list ) { { compound-requirement } -> type-constraint; }          // The result of compound-requirement satisfies type-constraint
requires ( parameter-list ) { { compound-requirement } noexcept -> type-constraint; } // The result of compound-requirement satisfies type-constraint and does not throw an exception

For example, the EqualityComparable concept could be implemented like this:

template<class T, class U>
concept Same = is_same_v<T, U>;

template<class T>
concept EqualityComparable = requires (const T & a, const T & b) {
    { a == b } -> Same<bool>;
    { a != b } -> Same<bool>;
};

template<class T, class U>

concept Same = is_same_v<T, U>;

template<class T>

concept EqualityComparable = requires (const T & a, const T & b) {

{ a == b } -> Same<bool>;

{ a != b } -> Same<bool>;

};

The EqualityComparable concept uses two compound requirements to check if an object of type T defines the == and != operators and that those operators return a bool result.

Notice that the semicolon comes at the end of the compound requirement. There is no semicolon inside the body of the compound requirement.

Nested Requirement

A nested requirement is used to test a constraint expression inside of a parent requires expression. The constraint expression of a nested requirement can use any of the local parameters introduced in any one of the the parent requires expression.

A nested requirement can have one of the following forms:

requires { requires constraint-expression; }
requires ( parameter-list ) { requires constraint-expression; }

Similar to the constraint expression of the concept definition, The constraint expression of a nested requirement is a logical set of boolean expression that consist of conjunctions (&&) and disjunctions (||) that are evaluated at compile-time to true if the constraint is satisfied or false otherwise.

The constraint expression can be:

A C++ (compile-time) expression that evaluates to true or false
A type trait that evaluates to true or false
A concept expression
A requires expression

Using nested requirements, it is technically possible to create atrocities such as this (but please don’t do this in your own code):

template<class T, class U>
concept Same = is_same_v<T, U>; // Uses is_same type trait.

template<class T>
concept AddressOf = requires (T t) {             // Requires expression
    requires requires (T u) {                    // Nested requirement
        requires requires (T v) {                // Nested requirement
            requires requires (T w) {            // Nested requirement
                requires Same<T*, decltype(&w)>; // Concept expression
            };
        };
    };
};

template<class T, class U>

concept Same = is_same_v<T, U>; // Uses is_same type trait.

template<class T>

concept AddressOf = requires (T t) { // Requires expression

requires requires (T u) { // Nested requirement

requires requires (T v) { // Nested requirement

requires requires (T w) { // Nested requirement

requires Same<T*, decltype(&w)>; // Concept expression

};

This of course can be simplified to just a single nested requirement:

template<class T, class U>
concept Same = is_same_v<T, U>;

template<class T>
concept AddressOf = requires (T t) {
    requires Same<T*, decltype(&t)>;
};

template<class T, class U>

concept Same = is_same_v<T, U>;

template<class T>

concept AddressOf = requires (T t) {

requires Same<T*, decltype(&t)>;

};

The AddressOf concept uses a nested requirement that, in turn, uses a concept expression to verify that the address of (&) operator applied to an instance of T results in T*. This concept is useful to check if T does not overload the address of operator to return a different type than expected.

std::addressof was added in C++11 to obtain the actual address of an object, even in the presence of an overloaded address of operator (&).

Requires Clause

The requires clause can be placed after the template parameter list in a class template or a function template definition. The template parameter list and the requires clause together form the template head. A template definition that uses a requires clause has this form:

template< parameter-list > requires constraint-expression
template body;

Notice that the requires clause is not terminated by a semicolon but any sub expressions of the constraint expression are.

The constraint expression of the requires clause is analogous to the constraint expression of the concept definition and the requires expression. That is, the constraint expression is a logical set of boolean expressions consisting of conjunctions (&&) or disjunctions (||) of one or more constant expressions that evaluate to true or false at compile time. The boolean expressions can be:

A C++ (compile-time) primary expression that evaluates to true or false
A type trait that evaluates to true or false
A concept expression
A requires expression

Using the same example from before, the following example shows that it is possible to used a nested requires expression in the requires clause:

template<typename T> requires requires (T t) {
    requires requires (T u) {
        requires requires (T v) {
            requires Same<T*, decltype(&v)>;
        };
    };
}
T* addressof(T& t)
{
    return &t;
}

template<typename T> requires requires (T t) {

requires requires (T u) {

requires requires (T v) {

requires Same<T*, decltype(&v)>;

};

}

T* addressof(T& t)

{

return &t;

}

I don’t recommend you use this in your own code. I recommend you use std::addressof instead. The example shown here demonstrates that you can use nested requires expressions in a requires clause.

The requires keyword appears twice in the template head because the first one introduces the requires clause and the second one introduces a requires expression.

Using a requires clause, we can constrain the template arguments that are used in the max function template from the Function Templates section above:

template<typename T, typename U> requires requires (T a, U b) { { a > b } -> Same<bool>; }
auto max(T a, U b) -> remove_reference_t<decltype(a > b ? a : b)>
{
    return a > b ? a : b;
}

template<typename T, typename U> requires requires (T a, U b) { { a > b } -> Same<bool>; }

auto max(T a, U b) -> remove_reference_t<decltype(a > b ? a : b)>

{

return a > b ? a : b;

}

Trying to use the max function template with a types that do not define the greater than operator (>) will result in a compiler error that states something like “the associated constraints are not satisfied”. It should be possible to improve this diagnostic error message by creating a named concept definition:

template<class T, class U>
concept Same = is_same_v<T, U>;

template<typename T, typename U>
concept GreaterThanComparableWith = requires (T a, U b) { { a > b } -> Same<bool>; };

template<typename T, typename U> requires GreaterThanComparableWith<T, U>
auto max(T a, U b) -> remove_reference_t<decltype(a > b ? a : b)>
{
    return a > b ? a : b;
}

template<class T, class U>

concept Same = is_same_v<T, U>;

template<typename T, typename U>

concept GreaterThanComparableWith = requires (T a, U b) { { a > b } -> Same<bool>; };

template<typename T, typename U> requires GreaterThanComparableWith<T, U>

auto max(T a, U b) -> remove_reference_t<decltype(a > b ? a : b)>

{

return a > b ? a : b;

}

Ideally, the compiler should generate better diagnostics when using named concepts. At the time of this writing, only the GCC compiler mentions the constraint that is being violated. Regardless, you should prefer to use named constraints in a requires clause to improve the compiler diagnostic error messages (at least, in the future).

It is also possible to specify the requires clause after the parameter list of a function declaration. For example, the two function template definitions are identical:

// Regular requires clause
template<typename T, typename U> requires GreaterThanComparableWith<T, U>
auto max(T a, U b)
{
    return a > b ? a : b;
}

// Trailing requires clause
template<typename T, typename U>
auto max(T a, U b) requires GreaterThanComparableWith<T, U>
{
    return a > b ? a : b;
}

// Regular requires clause

template<typename T, typename U> requires GreaterThanComparableWith<T, U>

auto max(T a, U b)

{

return a > b ? a : b;

}

// Trailing requires clause

template<typename T, typename U>

auto max(T a, U b) requires GreaterThanComparableWith<T, U>

{

return a > b ? a : b;

}

The second form of the max function template uses a trailing requires clause. It is also possible to combine a regular requires clause with a trailing requires clause in the same function template declaration. This will come in handy when we want to constrain the template parameters of a member function template of a class template.

Shorthand Notation

Instead of using a requires clause, a constraint can be placed directly on a template parameter. A named concept can be used in the template parameter list instead of typename (or class).

For example, the max function template can be written without the requires clause:

template<typename T, GreaterThanComparableWith<T> U>
auto max(T a, U b) -> remove_reference_t<decltype(a > b ? a : b)>
{
    return a > b ? a : b;
}

template<typename T, GreaterThanComparableWith<T> U>

auto max(T a, U b) -> remove_reference_t<decltype(a > b ? a : b)>

{

return a > b ? a : b;

}

In the above example, the second template parameter becomes GreaterThanComparableWith<T> U which moves the type constraint out of the requires clause and places the constraint directly on the type of U. This shorthand notation also allows us to omit the first template parameter from the named concept. In this case, U is implicitly used as the first argument to GreaterThanComparableWith and T is explicitly used as the second argument. That is, GreaterThanComparableWith<T> U (when used in the template parameter list) is equivalent to GreaterThanComparableWith<U, T> (when used in the requires clause).

The astute reader will realize that the shorthand notation, used in this way, changes the result of the concept. Instead of checking for the validity of a > b (as was the case when using the requires clause), the concpet now checks b > a which may not be the intention and may fail. To fix this issue, you could swap the order of the types in the template parameter list:

template<typename U, GreaterThanComparableWith<U> T>
auto max(T a, U b) -> remove_reference_t<decltype(a > b ? a : b)>
{
    return a > b ? a : b;
}

template<typename U, GreaterThanComparableWith<U> T>

auto max(T a, U b) -> remove_reference_t<decltype(a > b ? a : b)>

{

return a > b ? a : b;

}

Which would be fine if the end user relies on implicit type deduction. If the end user tries to specify the types explicitly, but gets the order of the types wrong, this could result in unintended behaviour.

The following is not allowed:

template<GreaterThanComparableWith<U> T, GreaterThanComparableWith<T> U>
auto max(T a, U b) -> remove_reference_t<decltype(a > b ? a : b)>
{
    return a > b ? a : b;
}

template<GreaterThanComparableWith<U> T, GreaterThanComparableWith<T> U>

auto max(T a, U b) -> remove_reference_t<decltype(a > b ? a : b)>

{

return a > b ? a : b;

}

The first occurrence of GreaterThanComparableWith<U> on line 7 will fail since U was not defined yet.

If the concept expression only applies to a single template parameter, then the template argument on the constraint can be omitted:

template<typename T>
concept Increment = requires (T a) { ++a; a++; };

template<Increment T>
T increment(T a)
{
    return ++a;
}

template<typename T>

concept Increment = requires (T a) { ++a; a++; };

template<Increment T>

T increment(T a)

{

return ++a;

}

In this case, the type T is constrained with the Increment concept. Since Increment only applies to a single template parameter, using the shorthand notation, T is used as an implicit template argument and can be omitted.

Constrained Class Templates

Constraining the template prameters of a class template is similar to that of a function template.

If you recall from the section about template arguments versus template parameters, we defined a simple Array class template. We can now constrain the types that can be used with the Array class template.

template<typename T, size_t N>
requires std::default_initializable<T> && std::destructible<T>
class Array
{
public:
    Array()
        : m_Data{}
    {}

    size_t size() const
    {
        return N;
    }

    T& operator[](size_t i)
    {
        assert(i < N);

        return m_Data[i];
    }

    const T& operator[](size_t i) const
    {
        assert(i < N);

        return m_Data[i];
    }

private:
    T m_Data[N];
};

template<typename T, size_t N>

requires std::default_initializable<T> && std::destructible<T>

class Array

{

public:

Array()

: m_Data{}

{}

size_t size() const

{

return N;

}

T& operator[](size_t i)

{

assert(i < N);

return m_Data[i];

}

const T& operator[](size_t i) const

{

assert(i < N);

return m_Data[i];

}

private:

T m_Data[N];

};

std::default_initializable is a concept which checks if the type can be created using a default constructor. This eliminates types that have an inaccessible default constructor (because it is either deleted, protected, or private to the class). Additionally, the std::destructible concept checks if a type can be safely destroyed at the end of its lifetime.

If you want to define the member functions of a class template outside of the class declaration, you must repeat the requires clause.

// Array header file.
template<typename T, size_t N> 
requires std::default_initializable<T> && std::destructible<T>
class Array
{
public:
    Array();

    size_t size() const;
	
	...
};

// Array implementation file.
template<typename T, size_t N>
requires std::default_initializable<T> && std::destructible<T>
Array<T, N>::Array()
    : m_Data{}
{}

template<typename T, size_t N>
requires std::default_initializable<T>&& std::destructible<T>
size_t Array<T, N>::size() const
{
    return N;
}

// Array header file.

template<typename T, size_t N>

requires std::default_initializable<T> && std::destructible<T>

class Array

{

public:

Array();

size_t size() const;

...

};

// Array implementation file.

template<typename T, size_t N>

requires std::default_initializable<T> && std::destructible<T>

Array<T, N>::Array()

: m_Data{}

{}

template<typename T, size_t N>

requires std::default_initializable<T>&& std::destructible<T>

size_t Array<T, N>::size() const

{

return N;

}

This example shows the Array constructor and size member functions are defined outside of the Array declaration. In this case, the template head (including the requires clause) must be repeated for each of the member functions of the class template.

Constrained Class Members

It can happen that you need to specify additional constraints on the member functions of a class template. For example, if we wanted to implement copy semantics on the Array class template, we would need to specify additional constraints the copy constructor and the assignment operator of the Array class:

// Array header file.
template<typename T, size_t N>
requires std::default_initializable<T> && std::destructible<T>
class Array
{
public:
    Array();

    Array(const Array & copy) requires std::copyable<T>;

    Array& operator=(const Array& rhs) requires std::copyable<T>;

	...
};

// Array implementation file.
template<typename T, size_t N>
requires std::default_initializable<T> && std::destructible<T>
Array<T, N>::Array()
   : m_Data{}
{}

template<typename T, size_t N>
requires std::default_initializable<T>&& std::destructible<T>
Array<T, N>::Array(const Array& copy) requires std::copyable<T>
{
   std::ranges::copy_n(copy.m_Data, N, m_Data);
}

template<typename T, size_t N>
requires std::default_initializable<T>&& std::destructible<T>
Array<T, N>& Array<T, N>::operator=(const Array& rhs) requires std::copyable<T>
{
    if (&rhs != this)
    {
        std::ranges::copy_n(rhs.m_Data, N, m_Data);
    }
    return *this;
}

// Array header file.

template<typename T, size_t N>

requires std::default_initializable<T> && std::destructible<T>

class Array

{

public:

Array();

Array(const Array & copy) requires std::copyable<T>;

Array& operator=(const Array& rhs) requires std::copyable<T>;

...

};

// Array implementation file.

template<typename T, size_t N>

requires std::default_initializable<T> && std::destructible<T>

Array<T, N>::Array()

: m_Data{}

{}

template<typename T, size_t N>

requires std::default_initializable<T>&& std::destructible<T>

Array<T, N>::Array(const Array& copy) requires std::copyable<T>

{

std::ranges::copy_n(copy.m_Data, N, m_Data);

}

template<typename T, size_t N>

requires std::default_initializable<T>&& std::destructible<T>

Array<T, N>& Array<T, N>::operator=(const Array& rhs) requires std::copyable<T>

{

if (&rhs != this)

{

std::ranges::copy_n(rhs.m_Data, N, m_Data);

}

return *this;

}

Although the code is starting to look a bit unwieldy, the example demonstrates that:

The requires clause after the template parameter list constrains the class template parameters.
The requires clause after the member function can further constrain the types. These constraints are only checked if the member function is instantiated.
The requires clause on the class template parameter list and the member function must be repeated in the definition of the member function (when defined outside the class declaration)

Concept-Based SFINAE

Similar to how the enable_if utility template is used to SFINAE-out function overloads, we can now use concepts instead. To demonstrate this, we’ll modify the Scalar class template from the SFINAE with enable_if example above. First, we’ll define a few concepts that mimic the is_int, is_float, and is_double type traits:

template<typename T>
concept Int = is_int_v<T>;

template<typename T>
concept Float = is_float_v<T>;

template<typename T>
concept Double = is_double_v<T>;

template<typename T>

concept Int = is_int_v<T>;

template<typename T>

concept Float = is_float_v<T>;

template<typename T>

concept Double = is_double_v<T>;

In the previous example, we used enable_if as an additional template parameter to SFINAE-out the constructor of the Scalar class based on the template argument type. Using concepts and the shorthand notation, this can be written much more succinctly:

class Scalar
{
    ...
public:
    template<Int I>
    Scalar(I i)
        : m_Type(Type::Integer)
        , m_Int(i)
    {}

    template<Float F>
    Scalar(F f)
        : m_Type(Type::Float)
        , m_Float(f)
    {}

    template<Double D>
    Scalar(D d)
        : m_Type(Type::Double)
        , m_Double(d)
    {}

class Scalar

{

...

public:

template<Int I>

Scalar(I i)

: m_Type(Type::Integer)

, m_Int(i)

{}

template<Float F>

Scalar(F f)

: m_Type(Type::Float)

, m_Float(f)

{}

template<Double D>

Scalar(D d)

: m_Type(Type::Double)

, m_Double(d)

{}

Instead of adding an additional template parameter using enable_if, we can constrain the template parameter directly using a named concept in the template parameter list. I hope you agree that using concepts to choose the correct function overload is much nicer looking than using enable_if.

The other functions of the Scalar class can also be improved using the same technique:

    template<Int I>
    void set(I i)
    {
        assert(m_Type == Type::Integer);
        m_Int = i;
    }

    template<Float F>
    void set(F f)
    {
        assert(m_Type == Type::Float);
        m_Float = f;
    }

    template<Double D>
    void set(D d)
    {
        assert(m_Type == Type::Double);
        m_Double = d;
    }

    template<Int I>
    I get() const
    {
        assert(m_Type == Type::Integer);
        return m_Int;
    }

    template<Float F>
    F get() const
    {
        assert(m_Type == Type::Float);
        return m_Float;
    }

    template<Double D>
    D get() const
    {
        assert(m_Type == Type::Double);
        return m_Double;
    }

template<Int I>

void set(I i)

{

assert(m_Type == Type::Integer);

m_Int = i;

}

template<Float F>

void set(F f)

{

assert(m_Type == Type::Float);

m_Float = f;

}

template<Double D>

void set(D d)

{

assert(m_Type == Type::Double);

m_Double = d;

}

template<Int I>

I get() const

{

assert(m_Type == Type::Integer);

return m_Int;

}

template<Float F>

F get() const

{

assert(m_Type == Type::Float);

return m_Float;

}

template<Double D>

D get() const

{

assert(m_Type == Type::Double);

return m_Double;

}

No more extraneous template parameters, function arguments, or ugly return types using enable_if when named concepts will suffice.

I realize that the Scalar class is a contrived example that could be solved with just regular function overloading or if constexpr. Regardless, I hope you have a better understanding of how concepts can be used to choose function overloads based on type traits.

Constraining Auto & Abbreviated Function Templates

Concepts can be used to constrain auto. Wherever auto can be used, Concept auto can also be used (where Concept is a previously defined named concept).

For example, suppose we have the following function template:

template<typename T>
concept Arithmetic = is_arithmetic_v<T>;

template<Arithmetic T, Arithmetic U>
auto add(T a, U b)
{
    return a + b;
}

template<typename T>

concept Arithmetic = is_arithmetic_v<T>;

template<Arithmetic T, Arithmetic U>

auto add(T a, U b)

{

return a + b;

}

This form of the add function uses the shorthand notation to place constraints on the types T and U. This function can also be written as an abbreviated function template:

auto add(Arithmetic auto a, Arithmetic auto b)
{
    return a + b;
}

auto add(Arithmetic auto a, Arithmetic auto b)

{

return a + b;

}

The abbreviated function template notation replaces the template parameter list with constrained auto function parameters.

Note: You can also use abbreviated function templates without constraints.

Constraints can also be placed on the return value of the function:

Arithmetic auto add(Arithmetic auto a, Arithmetic auto b)
{
    return a + b;
}

Arithmetic auto add(Arithmetic auto a, Arithmetic auto b)

{

return a + b;

}

We can further constrain the function parameters using a trailing requires clause, but when using abbreviated function templates, we need to use the decltype specifier to get at the underlying type:

template<class T, class U>
concept Addable = requires (const T& t, const U& u) {
    t + u;
};

Arithmetic auto add(Arithmetic auto a, Arithmetic auto b) requires Addable<decltype(a), decltype(b)>
{
    return a + b;
}

template<class T, class U>

concept Addable = requires (const T& t, const U& u) {

t + u;

};

Arithmetic auto add(Arithmetic auto a, Arithmetic auto b) requires Addable<decltype(a), decltype(b)>

{

return a + b;

}

You may argue that if a and b are Arithmetic types, then they will also be Addable. The example demonstrates how to specify additional requirements when using abbreviated function templates.

And we can also constrain the expected return value of a function:

Arithmetic auto i = add(3, 5);
Arithmetic auto j = add(3.0, 5);
Arithmetic auto k = add(3, 5.0f);

Arithmetic auto i = add(3, 5);

Arithmetic auto j = add(3.0, 5);

Arithmetic auto k = add(3, 5.0f);

In the above example, i, j, and k are constrained to be valid Arithmetic types (see is_arithmetic for more information) and the return value from the add function template is determined by the types of the arguments (which must also be arithmetic types).

Conclusion

A lot was covered in this article and if you got this far then congratulations! You are now an expert on C++ templates. You learned about value categories, template arguments and template parameters, function templates, class templates, and variable templates. You also learned about the many uses of the typename keyword and how to specialize templates. You’ve also seen example of using variadic templates and how to use a template parameter pack to implement recursive function templates.

You also learned how to use the decltype specifier and std::declval to form correct template expressions. You were bombarded with a set of (almost) 40 type traits that can be used to query or transform your template types and give you the tools needed to specify a set of constraints on template arguments. This article doesn’t even cover half of the type traits that are available in the standard template library (see type_traits for more information).

You learned about SFINAE and the various ways to utilize SFINAE to implement more complex type traits. You also learned about the various ways that enable_if can be used to specifiy constraints on template arguments. And finally, you learned about C++20 Concepts that allow you to specify constraints on template arguments without using enable_if.

As an added bonus, you also learned about abbreviated function templates that lets you write (constrained) function templates using a very succinct syntax.

But despite covering all of these topics, there are still a few that I’d like to cover:

Typelists
Type erasure

And possibly a few more templates related topics that I can’t even think of right now. In any case, I think this article provides a good foundation for getting started with C++ templates and template meta programming. Thanks for reading, and please leave a comment if you notice any omissions or corrections or if you can think of any templates related topics that you’d like me to cover.

Bibliography

[1] D. Vandevoorde, N. M. Josuttis, and D. Gregor, C++ templates: the complete guide, Second edition. Boston: Addison-Wesley, 2018.
[2] B. Stroustrup, “‘New’ Value Terminology.” Accessed: Jul. 06, 2020. [Online]. Available: https://www.stroustrup.com/terminology.pdf.
[3] “Value categories – cppreference.com.” https://en.cppreference.com/w/cpp/language/value_category (accessed Jul. 06, 2020).
[4] “Understanding lvalues and rvalues in C and C++ – Eli Bendersky’s website.” https://eli.thegreenplace.net/2011/12/15/understanding-lvalues-and-rvalues-in-c-and-c (accessed Jul. 06, 2020).
[5] “C++11 Tutorial: Explaining the Ever-Elusive Lvalues and Rvalues,” SmartBear.com. https://smartbear.com/blog/develop/c11-tutorial-explaining-the-ever-elusive-lvalues-a/ (accessed Jul. 06, 2020).
[6] W. M. Miller, “A Taxonomy of Expression Value Categories,” p. 20.
[7] S. Meyers, Effective modern C++: 42 specific ways to improve your use of C++11 and C++14, First edition. Beijing ; Sebastopol, CA: O’Reilly Media, 2014.
[8] “Universal References in C++11 — Scott Meyers : Standard C++.” https://isocpp.org/blog/2012/11/universal-references-in-c11-scott-meyers (accessed May 16, 2021).
[9] I. Horton and P. van Weert, Beginning C++20: from novice to professional. 2020.
[10] “c++ – How is std::is_function implemented?,” Stack Overflow. https://stackoverflow.com/questions/59654482/how-is-stdis-function-implemented (accessed Apr. 29, 2021).
[11] “c++ – What is std::decay and when it should be used?,” Stack Overflow. https://stackoverflow.com/questions/25732386/what-is-stddecay-and-when-it-should-be-used (accessed May 13, 2021).
[12] Cᐩᐩ Weekly With Jason Turner, C++ Weekly – Ep 189 – C++14’s Variable Templates, (Oct. 14, 2019). Accessed: Apr. 13, 2021. [Online Video]. Available: https://www.youtube.com/watch?v=2kY-go52rNw
[13] “Constraints and concepts (since C++20) – cppreference.com.” https://en.cppreference.com/w/cpp/language/constraints (accessed May 21, 2021).
[14] “Expressions – cppreference.com.” https://en.cppreference.com/w/cpp/language/expressions (accessed Jul. 06, 2020).
[15] “Function Templates Partial Specialization in C++,” Fluent C++, Aug. 15, 2017. https://www.fluentcpp.com/2017/08/15/function-templates-partial-specialization-cpp/ (accessed Mar. 30, 2021).
[16] gcc-mirror/gcc. gcc-mirror, 2021. Accessed: Apr. 06, 2021. [Online]. Available: https://github.com/gcc-mirror/gcc
[17] llvm/llvm-project. LLVM, 2021. Accessed: Apr. 06, 2021. [Online]. Available: https://github.com/llvm/llvm-project
[18] microsoft/STL. Microsoft, 2021. Accessed: Apr. 06, 2021. [Online]. Available: https://github.com/microsoft/STL
[19] B. Stroustrup, “‘New’ Value Terminology.” Accessed: Jul. 06, 2020. [Online]. Available: https://www.stroustrup.com/terminology.pdf
[20] “SFINAE – cppreference.com.” https://en.cppreference.com/w/cpp/language/sfinae (accessed May 21, 2021).
[21] “Singleton.” https://refactoring.guru/design-patterns/singleton (accessed Apr. 19, 2021).
[22] “Template parameters and template arguments – cppreference.com.” https://en.cppreference.com/w/cpp/language/template_parameters (accessed Mar. 31, 2021).
[23] “Type alias, alias template (since C++11) – cppreference.com.” https://en.cppreference.com/w/cpp/language/type_alias (accessed Apr. 13, 2021).
[24] “Yet another type-trait: decay.” http://www.open-std.org/jtc1/sc22/wg21/docs/papers/2006/n2069.html (accessed May 13, 2021).

3 thoughts on “C++ Template Programming”

stephane on July 23, 2022 at 12:17 pm said:

Best resources I ever found

Reply ↓
Robert on January 23, 2023 at 1:24 pm said:

Amazing, so helpful and informative.

Reply ↓
Hari on June 28, 2023 at 7:32 am said:

Appreciate the effort that has gone into this tutorial.

Reply ↓